题目内容
19.我们知道,$\sqrt{{a}^{2}}$=|a|,那么要化简$\sqrt{4+2\sqrt{3}}$必须将被开方数变形为${(\sqrt{a}+\sqrt{b})}^{2}$的形式,若4+2$\sqrt{3}$=${(\sqrt{a}+\sqrt{b})}^{2}$,则4+2$\sqrt{3}$=a+b+2$\sqrt{ab}$,令$\left\{\begin{array}{l}{a+b=4}\\{ab=3}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=1}\\{b=3}\end{array}\right.$或$\left\{\begin{array}{l}{a=3}\\{b=1}\end{array}\right.$,故$\sqrt{4+2\sqrt{3}}$=$\sqrt{{(\sqrt{3}+1)}^{2}}$=$\sqrt{3}+1$.化简下列各式:
(1)$\sqrt{7-2\sqrt{10}}$;
(2)$\sqrt{8-4\sqrt{3}}$;
(3)$\sqrt{2-\sqrt{3}}$;
(4)$\sqrt{5+2\sqrt{6}}$+$\sqrt{5-2\sqrt{6}}$.
分析 (1)根据题意结合完全平方公式开平方得出即可;
(2)根据题意结合完全平方公式开平方得出即可;
(3)根据题意结合完全平方公式开平方得出即可;
(4)根据题意结合完全平方公式开平方得出即可.
解答 解:(1)$\sqrt{7-2\sqrt{10}}$=$\sqrt{(\sqrt{5}-\sqrt{2})^{2}}$=$\sqrt{5}$-$\sqrt{2}$;
(2)$\sqrt{8-4\sqrt{3}}$
=$\sqrt{2(4-2\sqrt{3})}$
=$\sqrt{2(2-\sqrt{3})^{2}}$
=(2-$\sqrt{3}$)$\sqrt{2}$
=2$\sqrt{2}$-$\sqrt{6}$;
(3)$\sqrt{2-\sqrt{3}}$=$\sqrt{\frac{4-2\sqrt{3}}{2}}$=$\frac{\sqrt{(2-\sqrt{3})^{2}}}{\sqrt{2}}$=$\frac{2-\sqrt{3}}{\sqrt{2}}$=$\frac{2\sqrt{2}-\sqrt{6}}{2}$;
(4)$\sqrt{5+2\sqrt{6}}$+$\sqrt{5-2\sqrt{6}}$
=$\sqrt{\frac{10+4\sqrt{6}}{2}}$+$\sqrt{\frac{10-4\sqrt{6}}{2}}$
=$\sqrt{\frac{(2+\sqrt{6})^{2}}{2}}$+$\sqrt{\frac{(2-\sqrt{6})^{2}}{2}}$
=$\frac{\sqrt{2}}{2}$×(2+$\sqrt{6}$)+$\frac{\sqrt{2}}{2}$×(2-$\sqrt{6}$)
=2$\sqrt{2}$.
点评 此题主要考查了二次根式的化简,正确利用完全平方公式得出是解题关键.

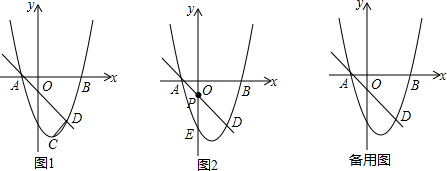

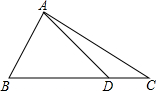 如图,在△ABC中,D是边BC上一点,BD=3DC,$\overrightarrow{BA}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,那么$\overrightarrow{AD}$=$\frac{3}{4}$$\overrightarrow{b}$-$\overrightarrow{a}$(用向量$\overrightarrow{a}$、$\overrightarrow{b}$来表示).
如图,在△ABC中,D是边BC上一点,BD=3DC,$\overrightarrow{BA}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,那么$\overrightarrow{AD}$=$\frac{3}{4}$$\overrightarrow{b}$-$\overrightarrow{a}$(用向量$\overrightarrow{a}$、$\overrightarrow{b}$来表示).