题目内容
9.已知:3(a2+b2+c2)=(a+b+c)2,求证:a=b=c.分析 首先利用完全平方公式计算,进一步合并整理后,因式分解得出结论即可.
解答 证明:∵3(a2+b2+c2)=(a+b+c)2,
∴3(a2+b2+c2)-(a2+2ab+b2+2ac+2bc+c2)=0,
∴2a2-2ab+2b2-2ac-2bc+c2=0,
∴(a-b)2+(b-c)2+(a-c)2=0
∴a-b=0,b-c=0,a-c=0,
∴a=b,b=c,c=a,
∴a=b=c.
点评 此题考查因式分解的实际运用,利用完全平方公式因式分解和非负数的性质是解决问题的关键.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
1.已知x2-3x+1=0,则x4+$\frac{1}{x^{4}}$的值为( )
| A. | 7 | B. | 47 | C. | 9 | D. | 49 |
19.在一次学生田径运动会上,参加跳高的15名运动员的成绩如下表所示:
那么这些运动员跳高成绩的众数是( )
| 成绩(m) | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 |
| 人数 | 1 | 1 | 3 | 5 | 3 | 2 |
| A. | 3 | B. | 5 | C. | 1.65 | D. | 1.70 |
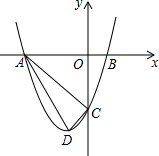 二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A(-3,0)、B(1,0)两点,与y轴交于点C(0,-3m)(其中m>0),顶点为D.
二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A(-3,0)、B(1,0)两点,与y轴交于点C(0,-3m)(其中m>0),顶点为D.