题目内容
4．设M=x2-8x+20，N=-x2+4x-3，比较M与N的大小．分析 利用求差法比较代数式的大小：计算M-N的值，通过配方得到M-N=2（x-3）2+5，再根据非负数的性质得到M-N＞0，于是可判断M与N的大小．
解答 解：M-N=x2-8x+20-（-x2+4x-3）
=2x2-12x+23
=2（x-3）2+5，
∵2（x-3）2≥0，
∴2（x-3）2+5＞0，
∴M-N＞0，
即M＞N．
点评 本题考查了配方法的应用：用配方法解一元二次方程；利用配方法求二次三项式是一个完全平方式时所含字母系数的值．也考查了非负数的性质．注意利用求差法比较代数式的大小．
练习册系列答案
相关题目
14．“鑫鑫”商店经销甲、乙两种商品，第一季度销售这两种商品共获利12000元，且1月，2月，3月的总利润比为8：7：9，甲、乙两种商品的成本与售价如表所示：
请根据以上信息，解答下列问题：
（1）1月份的总利润为4000元；
（2）已知2月份甲商品的销售量比1月份增加了10%，乙商品的销售价比1月份减少了20%，请分别求出1月份甲、乙两种商品的销售量；
（3）若3月份该商店销售乙商品的数量不超过甲商品数量的3倍，求3月份甲商品销售量的最小值．
| 商品 | 成本价（元/个） | 销售价（元/个） |
| 甲 | 20 | 40 |
| 乙 | 30 | 60 |
（1）1月份的总利润为4000元；
（2）已知2月份甲商品的销售量比1月份增加了10%，乙商品的销售价比1月份减少了20%，请分别求出1月份甲、乙两种商品的销售量；
（3）若3月份该商店销售乙商品的数量不超过甲商品数量的3倍，求3月份甲商品销售量的最小值．
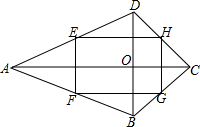如图，在四边形ABCD中，AC⊥DB，垂足为O，点E、F、G、H分别为AD、AB、BC、CD的中点，求证：四边形EFGH是矩形．