题目内容
17.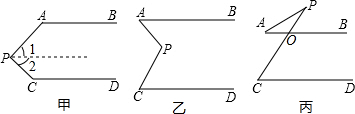 阅读下列解答过程:如图甲,AB∥CD,探索∠APC与∠BAP、∠PCD之间的关系.解:过点P作PE∥AB.
阅读下列解答过程:如图甲,AB∥CD,探索∠APC与∠BAP、∠PCD之间的关系.解:过点P作PE∥AB.∵AB∥CD,
∴PE∥AB∥CD(平行于同一条直线的两条直线互相平行).
∴∠1+∠A=180°(两直线平行,同旁内角互补),
∠2+∠C=180°(两直线平行,同旁内角互补).
∴∠1+∠A+∠2+∠C=360°.
又∵∠APC=∠1+∠2,
∴∠APC+∠A+∠C=360°.
如图乙和图丙,AB∥CD,请根据上述方法分别探索两图中∠APC与∠BAP、∠PCD之间的关系.
分析 图乙,过P作PE∥AB,求出AB∥PE∥CD,根据平行线的性质得出∠A=∠APE,∠C=∠CPE,即可求出答案;
图丙,根据平行线的性质得出∠PCD=∠POB,根据三角形外角性质求出∠POB=∠PAB+∠APC,即可求出答案.
解答 解:图乙,∠APC=∠A+∠C,
理由是:
过P作PE∥AB,
∵AB∥CD,
∴AB∥PE∥CD,
∴∠A=∠APE,∠C=∠CPE,
∴∠APC=∠APE+∠CPE=∠A+∠C;
图丙,∠APC=∠PCD-∠PAB,
理由是:∵AB∥CD,
∴∠PCD=∠POB,
∵∠POB=∠PAB+∠APC,
∴∠APC=∠POB-∠PAB=∠PCD-∠PAB.
点评 本题考查了平行线的性质和三角形外角性质的应用,能正确运用平行线的性质定理进行推理是解此题的关键.

练习册系列答案
相关题目
8.若427+41000+4n为完全平方数,则正整数n满足( )
| A. | n≥1972 | B. | n≤1972 | C. | n≥1973 | D. | n≤1970 |
5.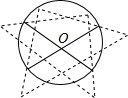 如图,用直角三角板经过两次画图找到圆形工件的圆心,这种方法应用的道理是( )
如图,用直角三角板经过两次画图找到圆形工件的圆心,这种方法应用的道理是( )
 如图,用直角三角板经过两次画图找到圆形工件的圆心,这种方法应用的道理是( )
如图,用直角三角板经过两次画图找到圆形工件的圆心,这种方法应用的道理是( )| A. | 垂径定理 | B. | 勾股定理 | ||
| C. | 直径所对的圆周角是直角 | D. | 90°的圆周角所对的弦是直径 |
12.下列说法:
①直径是弦;
②弦是直径;
③过圆上任意一点有无数条弦,且这些弦都相等;
④直径是圆中最长的弦.
其中正确的是( )
①直径是弦;
②弦是直径;
③过圆上任意一点有无数条弦,且这些弦都相等;
④直径是圆中最长的弦.
其中正确的是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
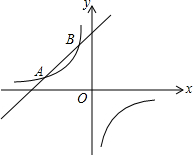 如图,已知反比例函数y1=$\frac{k}{x}$(k≠0)的图象经过点(8,-$\frac{1}{2}$),直线y2=x+b与反比例函数图象相交于点A和点B(m,4).
如图,已知反比例函数y1=$\frac{k}{x}$(k≠0)的图象经过点(8,-$\frac{1}{2}$),直线y2=x+b与反比例函数图象相交于点A和点B(m,4).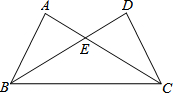 如图,△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.
如图,△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.