题目内容
如图，AB是⊙O的直径，直线AT切⊙O于点A，BT交⊙O于C，已知∠B=30°，AT=| 3 |
考点：切线的性质
专题：计算题
分析：连接AC，如图所示，由AT与圆O相切，得到BA垂直于AT，在直角三角形ABT中，利用锐角三角函数定义求出AB的长，根据AB为圆O的直径，利用直径所对的圆周角为直角得到∠ACB=90°，在直角三角形ABC中，利用锐角三角函数定义即可求出BC的长．
解答：
解：连接AC，如图所示：
∵直线AT切⊙O于点A，
∴∠BAT=90°，
在Rt△ABT中，∠B=30°，AT=
，
∴tan30°=
，即AB=
=3；
∵AB是⊙O的直径，
∴∠ACB=90°，
在Rt△ABC中，∠B=30°，AB=3，
∴cos30°=
，
则BC=AB•cos30°=
．
解：连接AC，如图所示：∵直线AT切⊙O于点A，
∴∠BAT=90°，
在Rt△ABT中，∠B=30°，AT=
| 3 |
∴tan30°=
| AT |
| AB |
| ||
| tan30° |
∵AB是⊙O的直径，
∴∠ACB=90°，
在Rt△ABC中，∠B=30°，AB=3，
∴cos30°=
| BC |
| AB |
则BC=AB•cos30°=
3
| ||
| 2 |
点评：此题考查了切线的性质，锐角三角函数定义，以及圆周角定理，熟练掌握切线的性质是解本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
如图，已知抛物线y=-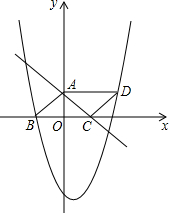
如图，△ABC是以BC为底边的等腰三角形，点A、C分别是一次函数
如图，已知A（1，0）和点B（-3，0），点C在y轴负半轴上，AC⊥BC，经过A，B，C三点的抛物线的对称轴分别交x轴、直线BC、直线AC于点F、E、M，