题目内容
19.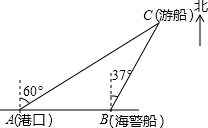 一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻事故,立即出发了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以50海里每小时的速度前往救援,求海警船到达事故船C处所需的大约时间.(温馨提示:sin53°≈0.8,cos53°≈0.6)
一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻事故,立即出发了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以50海里每小时的速度前往救援,求海警船到达事故船C处所需的大约时间.(温馨提示:sin53°≈0.8,cos53°≈0.6)
分析 作CH⊥AB于H,如图,根据题意得∠BAC=30°,∠HBC=53°,先在Rt△ACH中,利用正弦的定义求出CH=40,再在Rt△BCH中利用正弦的定义求出BC,然后利用速度公式求出海警船到达事故船C处所需时间.
解答 解:作CH⊥AB于H,如图,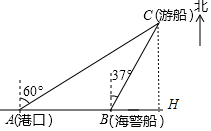
根据题意得∠BAC=30°,∠HBC=90°-37°=53°,AC=80,
在Rt△ACH中,∵sinA=$\frac{CH}{AC}$,
∴CH=ACtanA=80•sin30°=40,
在Rt△BCH中,∵sin∠CBH=$\frac{CH}{CB}$,
∴CB=$\frac{CH}{sin∠CBH}$=$\frac{40}{sin53°}$≈50,
∴海警船到达事故船C处所需为$\frac{50}{50}$=1(小时).
答:海警船到达事故船C处所需的大约为1小时.
点评 本题考查了解直角三角形的应用:解决此类问题要了解角之间的关系,找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作高或垂线构造直角三角形,另当问题以一个实际问题的形式给出时,要善于读懂题意,把实际问题划归为直角三角形中边角关系问题加以解决.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
9.下列计算正确的是( )
| A. | a2+a2=a4 | B. | (a2)3=a5 | C. | 2a2-a2=2 | D. | a5•a2=a7 |
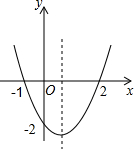 二次函数y=ax2+bx+c的图象如图所示,以下结论:①abc>0;②4ac<b2;③2a+b>0;④其顶点坐标为($\frac{1}{2}$,-2);⑤当x<$\frac{1}{2}$时,y随x的增大而减小;⑥a+b+c>0正确的有( )
二次函数y=ax2+bx+c的图象如图所示,以下结论:①abc>0;②4ac<b2;③2a+b>0;④其顶点坐标为($\frac{1}{2}$,-2);⑤当x<$\frac{1}{2}$时,y随x的增大而减小;⑥a+b+c>0正确的有( )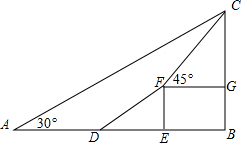 如图,为了测量某建筑物BC的高度,小明先在地面上用测角仪A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了20m到达D处,此时遇到一斜坡,坡度i=1:$\sqrt{3}$,沿着斜坡前进40m到达F处测得建筑物顶部的仰角是45°,(坡度i=1:$\sqrt{3}$是指坡面的铅直高度FE与水平宽度DE的比).
如图,为了测量某建筑物BC的高度,小明先在地面上用测角仪A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了20m到达D处,此时遇到一斜坡,坡度i=1:$\sqrt{3}$,沿着斜坡前进40m到达F处测得建筑物顶部的仰角是45°,(坡度i=1:$\sqrt{3}$是指坡面的铅直高度FE与水平宽度DE的比). 如图,四边形ABCD是平行四边形,E、F分别是BC、AD上的点,∠1=∠2.
如图,四边形ABCD是平行四边形,E、F分别是BC、AD上的点,∠1=∠2.