题目内容
11.先化简,再求值:($\frac{{x}^{2}-2x+4}{x-1}$+2-x)÷$\frac{{x}^{2}+4x+4}{x-1}$,其中x满足x2+2x-3=0.分析 首先将括号里面进行通分运算,进而利用分式除法运算法则计算得出答案.
解答 解:原式=$\frac{{x}^{2}-2x+4+(2-x)(x-1)}{x-1}$×$\frac{x-1}{(x+2)^{2}}$
=$\frac{1}{x+2}$,
∵x2+2x-3=0,
解得:x1=1,x2=-3,
又∵$\left\{\begin{array}{l}{x-1≠0}\\{x+2≠0}\end{array}\right.$,
∴x≠1且x≠-2,
∴x=-3,
∴原式=$\frac{1}{-3+2}$=-1.
点评 此题主要考查了分式的化简求值,正确进行分式的混合运算是解题关键.

练习册系列答案
相关题目
3.一次函数y=kx+2的图象经过1、2、4象限,当x>0时,函数值y的范围是( )
| A. | y=2 | B. | y>2 | C. | y<2 | D. | y≠2 |
 老师想知道学生每天在上学的路上要花多少时间,于是让大家将每天来学校的单程时间写在纸上.如图是全班30名学生上学单程所花时间的条形统计图:
老师想知道学生每天在上学的路上要花多少时间,于是让大家将每天来学校的单程时间写在纸上.如图是全班30名学生上学单程所花时间的条形统计图: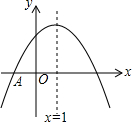 如图,抛物线y=ax2+bx+c与x轴交于点A(-1,0),顶点坐标(1,n),与y轴的交点在(0,3),(0,4)之间(包含端点),则下列结论:①abc>0;②3a+b<0;③-$\frac{4}{3}$≤a≤-1;④a+b≥am2+bm(m为任意实数);⑤一元二次方程ax2+bx+c=n有两个不相等的实数根,其中正确的有( )
如图,抛物线y=ax2+bx+c与x轴交于点A(-1,0),顶点坐标(1,n),与y轴的交点在(0,3),(0,4)之间(包含端点),则下列结论:①abc>0;②3a+b<0;③-$\frac{4}{3}$≤a≤-1;④a+b≥am2+bm(m为任意实数);⑤一元二次方程ax2+bx+c=n有两个不相等的实数根,其中正确的有( )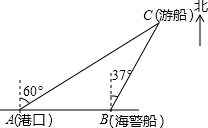 一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻事故,立即出发了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以50海里每小时的速度前往救援,求海警船到达事故船C处所需的大约时间.(温馨提示:sin53°≈0.8,cos53°≈0.6)
一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻事故,立即出发了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以50海里每小时的速度前往救援,求海警船到达事故船C处所需的大约时间.(温馨提示:sin53°≈0.8,cos53°≈0.6)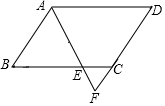 如图,在?ABCD中,AB=6,AD=9,∠BAD=120°且∠BAD的平分线交BC于点E,交DC的延长线于点F,则△CEF的周长为( )
如图,在?ABCD中,AB=6,AD=9,∠BAD=120°且∠BAD的平分线交BC于点E,交DC的延长线于点F,则△CEF的周长为( )