题目内容
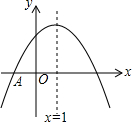
7.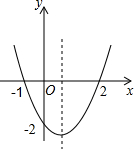 二次函数y=ax2+bx+c的图象如图所示,以下结论:①abc>0;②4ac<b2;③2a+b>0;④其顶点坐标为($\frac{1}{2}$,-2);⑤当x<$\frac{1}{2}$时,y随x的增大而减小;⑥a+b+c>0正确的有( )
二次函数y=ax2+bx+c的图象如图所示,以下结论:①abc>0;②4ac<b2;③2a+b>0;④其顶点坐标为($\frac{1}{2}$,-2);⑤当x<$\frac{1}{2}$时,y随x的增大而减小;⑥a+b+c>0正确的有( )| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
分析 根据二次函数的性质和二次函数的图象可以判断题目中各个小题的结论是否成立,从而可以解答本题.
解答 解:由图象可知,
抛物线开口向上,则a>0,顶点在y轴右侧,则b<0,与y轴交于负半轴,则c<0,
∴abc>0,故①正确,
函数图象与x轴有两个不同的交点,则b2-4ac>0,即4ac<b2,故②正确,
由图象可知,$-\frac{b}{2a}=\frac{-1+2}{2}=\frac{1}{2}$,则2b=-2a,2a+b=-b>0,故③正确,
由抛物线过点(-1,0),(0,-2),(2,0),可得,
$\left\{\begin{array}{l}{a×(-1)^{2}+b×(-1)+c=0}\\{c=-2}\\{a×{2}^{2}+2b+c=0}\end{array}\right.$,
得$\left\{\begin{array}{l}{a=1}\\{b=-1}\\{c=-2}\end{array}\right.$,
∴y=x2-x-2=$(x-\frac{1}{2})^{2}-\frac{9}{4}$,
∴顶点坐标是($\frac{1}{2}$,-$\frac{9}{4}$),故④错误,
∴当x<$\frac{1}{2}$时,y随x的增大而减小,故⑤正确,
当x=1时,y=a+b+c<0,故⑥错误,
由上可得,正确是①②③⑤,
故选B.
点评 本题考查二次函数图象与系数的关系,解答本题的关键是明确二次函数的性质,利用数形结合的思想解答.

练习册系列答案
相关题目
15.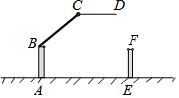 一小区大门的栏杆如图所示,当栏杆抬起时,BA垂直于地面AE,CD平行于地面AE,则∠ABC+∠BCD的度数为( )
一小区大门的栏杆如图所示,当栏杆抬起时,BA垂直于地面AE,CD平行于地面AE,则∠ABC+∠BCD的度数为( )
 一小区大门的栏杆如图所示,当栏杆抬起时,BA垂直于地面AE,CD平行于地面AE,则∠ABC+∠BCD的度数为( )
一小区大门的栏杆如图所示,当栏杆抬起时,BA垂直于地面AE,CD平行于地面AE,则∠ABC+∠BCD的度数为( )| A. | 180° | B. | 270° | C. | 300° | D. | 360° |
12.已知am=2,an=3,ap=4,则a2m+3n-p的值为( )
| A. | 36 | B. | 27 | C. | 9 | D. | 6 |
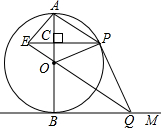 如图,AB是⊙O的直径,BM切⊙O于点B,点P是⊙O上的一个动点(点P不与A,B两点重合),连接AP,过点O作OQ∥AP交BM于点Q,过点P作PE⊥AB于点C,交QO的延长线于点E,连接PQ,OP.
如图,AB是⊙O的直径,BM切⊙O于点B,点P是⊙O上的一个动点(点P不与A,B两点重合),连接AP,过点O作OQ∥AP交BM于点Q,过点P作PE⊥AB于点C,交QO的延长线于点E,连接PQ,OP.
 如图,抛物线y=ax2+bx+c与x轴交于点A(-1,0),顶点坐标(1,n),与y轴的交点在(0,3),(0,4)之间(包含端点),则下列结论:①abc>0;②3a+b<0;③-$\frac{4}{3}$≤a≤-1;④a+b≥am2+bm(m为任意实数);⑤一元二次方程ax2+bx+c=n有两个不相等的实数根,其中正确的有( )
如图,抛物线y=ax2+bx+c与x轴交于点A(-1,0),顶点坐标(1,n),与y轴的交点在(0,3),(0,4)之间(包含端点),则下列结论:①abc>0;②3a+b<0;③-$\frac{4}{3}$≤a≤-1;④a+b≥am2+bm(m为任意实数);⑤一元二次方程ax2+bx+c=n有两个不相等的实数根,其中正确的有( )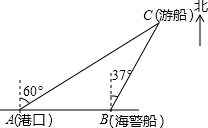 一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻事故,立即出发了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以50海里每小时的速度前往救援,求海警船到达事故船C处所需的大约时间.(温馨提示:sin53°≈0.8,cos53°≈0.6)
一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻事故,立即出发了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以50海里每小时的速度前往救援,求海警船到达事故船C处所需的大约时间.(温馨提示:sin53°≈0.8,cos53°≈0.6)