��Ŀ����
4��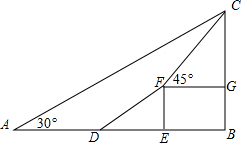 ��ͼ��Ϊ�˲���ij������BC�ĸ߶ȣ�С�����ڵ������ò����A����ý����ﶥ����������30�㣬Ȼ����ˮƽ������������ǰ����20m����D������ʱ����һб�£��¶�i=1��$\sqrt{3}$������б��ǰ��40m����F����ý����ﶥ����������45�㣬���¶�i=1��$\sqrt{3}$��ָ�����Ǧֱ�߶�FE��ˮƽ����DE�ıȣ���
��ͼ��Ϊ�˲���ij������BC�ĸ߶ȣ�С�����ڵ������ò����A����ý����ﶥ����������30�㣬Ȼ����ˮƽ������������ǰ����20m����D������ʱ����һб�£��¶�i=1��$\sqrt{3}$������б��ǰ��40m����F����ý����ﶥ����������45�㣬���¶�i=1��$\sqrt{3}$��ָ�����Ǧֱ�߶�FE��ˮƽ����DE�ıȣ�����1����б��DF�Ķ˵�F��ˮƽ����AB�ľ����б�µ�ˮƽ����DE�ֱ�Ϊ�����ף�
��2��������BC�ĸ߶�Ϊ�����ף�
��3����С���ڽ�����һ¥��ˮƽ�����ϵ�B�����˵�����¥������C���������ٶ�Ϊ2��$\sqrt{3}$+3��m/s��ͬʱС���Ӳ���Ǵ�����A����������Ħ�г���б�µĶ˵�F������֪��С����ƽ���ϵij��������³��ٵ�������С������ʱ����С������ʱ���һ�룬��С������ʱ�ij���Ϊ���٣�
���� ��1����Rt��Rt��DEF�У�DF=40��m����EF��DF=1��$\sqrt{3}$���Ƴ�tan��EDF=$\frac{\sqrt{3}}{3}$���ɵá�EDF=30�㣬�ɴ˼��ɽ�����⣻
��2����CG=GF=x����Rt��ABC�У���AB=$\sqrt{3}$BC���ɵ�20+20$\sqrt{3}$+x=$\sqrt{3}$��x+20�����ⷽ�̼��ɣ�
��3����С������ʱ�ij���Ϊym/s���������̼��ɽ�����⣻
��� �⣺��1����Rt��DEF�У�DF=40��m����EF��DF=1��$\sqrt{3}$��
��tan��EDF=$\frac{\sqrt{3}}{3}$��
���EDF=30�㣬
��EF=$\frac{1}{2}$DF=20��m����DE=$\sqrt{3}$EF=20$\sqrt{3}$��m����
��б��DF�Ķ˵�F��ˮƽ����AB�ľ���Ϊ20m��б�µ�ˮƽ����DEΪ20$\sqrt{3}$�ף�
��2����Rt��CGF�У��ߡ�CFG=45�㣬
��GC=GF����CG=GF=x��
��Rt��ABC����AB=$\sqrt{3}$BC��
��20+20$\sqrt{3}$+x=$\sqrt{3}$��x+20����
��x=10+10$\sqrt{3}$��
��BC=CG+BG=30+10$\sqrt{3}$��
��3����С������ʱ�ij���Ϊym/s��
������$\frac{30+10\sqrt{3}}{2��\sqrt{3}+3��}$=$\frac{1}{2}$��$\frac{20}{2Y}$+$\frac{40}{y}$����
���y=5��
�����飬y=5�Ƿ��̵Ľ⣬�ҷ������⣬
��С������ʱ�ij���Ϊ5m/s��
���� ���⿼���������븩�ǡ��¶ȡ���ֱ�������ε�֪ʶ֪ʶ�������Ѷ����У�ע���ܽ��������븩�ǹ���ֱ�������β���ֱ���������ǽ����Ĺؼ���ע���������ν��˼���뷽��˼���Ӧ�ã�

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�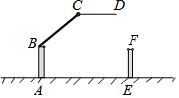 һС�����ŵ�������ͼ��ʾ��������̧��ʱ��BA��ֱ�ڵ���AE��CDƽ���ڵ���AE�����ABC+��BCD�Ķ���Ϊ��������
һС�����ŵ�������ͼ��ʾ��������̧��ʱ��BA��ֱ�ڵ���AE��CDƽ���ڵ���AE�����ABC+��BCD�Ķ���Ϊ��������| A�� | 180�� | B�� | 270�� | C�� | 300�� | D�� | 360�� |
| A�� | 36 | B�� | 27 | C�� | 9 | D�� | 6 |
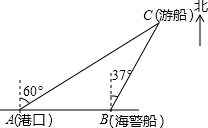 һ�ҹ۹��δ��Ӹۿ�A�Ա�ƫ��60��ķ�����۹۹⣬����80������C��ʱ�����˲෭�¹ʣ���������������źţ�һ���ڸۿ���������ĺ������ӵ�����źţ�����¹ʴ������ı�ƫ��37�㷽��������50����ÿСʱ���ٶ�ǰ����Ԯ�����������¹ʴ�C������Ĵ�Լʱ�䣮����ܰ��ʾ��sin53���0.8��cos53���0.6��
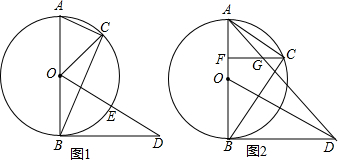
һ�ҹ۹��δ��Ӹۿ�A�Ա�ƫ��60��ķ�����۹۹⣬����80������C��ʱ�����˲෭�¹ʣ���������������źţ�һ���ڸۿ���������ĺ������ӵ�����źţ�����¹ʴ������ı�ƫ��37�㷽��������50����ÿСʱ���ٶ�ǰ����Ԯ�����������¹ʴ�C������Ĵ�Լʱ�䣮����ܰ��ʾ��sin53���0.8��cos53���0.6�� ��֪һ�κ���y=kx+b��ͼ����A��-3��0����B��2��5�����㣮����������y=kx��ͼ����B��2��3����
��֪һ�κ���y=kx+b��ͼ����A��-3��0����B��2��5�����㣮����������y=kx��ͼ����B��2��3����