题目内容
8．
如图，四边形ABCD是平行四边形，E、F分别是BC、AD上的点，∠1=∠2．求证：AF=CE．
分析 由四边形ABCD是平行四边形，得出∠B=∠D、AB=DC、AD=BC，再由ASA证得△ABE≌△CDF，得出BE=DF即可得出结论．
解答 证明：∵四边形ABCD是平行四边形，
∴∠B=∠D，AB=DC，AD=BC，
在△ABE和△CDF中，$\left\{\begin{array}{l}{∠1=∠2}\\{AB=DC}\\{∠B=∠D}\end{array}\right.$，
∴△ABE≌△CDF（ASA），
∴BE=DF
又∵AD=BC
∴AF=CE．
点评 本题主要考查了平行四边形的性质、全等三角形的判定与性质等知识，熟练掌握全等三角形的判定与性质是解决问题的关键．
练习册系列答案
相关题目
一艘观光游船从港口A以北偏东60°的方向出港观光，航行80海里至C处时发生了侧翻事故，立即出发了求救信号，一艘在港口正东方向的海警船接到求救信号，测得事故船在它的北偏东37°方向，马上以50海里每小时的速度前往救援，求海警船到达事故船C处所需的大约时间．（温馨提示：sin53°≈0.8，cos53°≈0.6）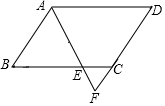
如图，在?ABCD中，AB=6，AD=9，∠BAD=120°且∠BAD的平分线交BC于点E，交DC的延长线于点F，则△CEF的周长为（ ）
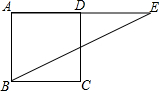如图，正方形ABCD的边长是3cm，在AD的延长线上有一点E，当BE=$\sqrt{21}$cm时，DE的长是2$\sqrt{3}$-3cm．