题目内容
若直线y=-x+b和两坐标轴围成两三角形面积为2，求b的值．
考点：一次函数图象上点的坐标特征
专题：
分析：先求出直线y=-x+b和两坐标轴的交点，再根据三角形的面积公式求解即可．
解答：解：∵令x=0，则y=b；令y=0，则x=b，
∴直线y=-x+b两坐标轴的交点分别为（0，b），（b，0），
∴
b2=2，
解得b=±2．
∴直线y=-x+b两坐标轴的交点分别为（0，b），（b，0），
∴
| 1 |
| 2 |
解得b=±2．
点评：本题考查的是一次函数图象上点的坐标特点，熟知直线与两坐标轴的交点是解答此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
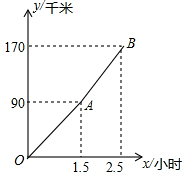“五一节”期间，王老师一家自驾游去了离家170千米的某地，下面是他们家的距离y（千米）与汽车行驶时间x（小时）之间的函数图象，当他们离目的地还有20千米时，汽车一共行驶的时间是（ ）| A、2小时 | B、2.2小时 |
| C、2.25小时 | D、2.4小时 |
在平行四边形ABCD中，对角线AC、BD相交于点O，如果AC=10，BD=8，AB=x，则x的取值范围是（ ）
| A、1＜x＜9 |
| B、2＜x＜18 |
| C、8＜x＜10 |
| D、4＜x＜5 |
高老师将九（1）班某次数学测验成绩分成0～25、26～50、51～75、76～100四组，制作了如下统计表：
