题目内容
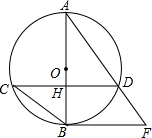 如图,AB为⊙O的直径,弦CD⊥AB于点H,过点B作⊙O的切线与AD的延长线交于F.
如图,AB为⊙O的直径,弦CD⊥AB于点H,过点B作⊙O的切线与AD的延长线交于F.(1)求证:∠ABC=∠F;
(2)若sinC=
| 3 |
| 5 |
考点:切线的性质,解直角三角形
专题:
分析:(1)由切线的性质得AB⊥BF,因为CD⊥AB,所以CD∥BF,由平行线的性质得∠ADC=∠F,由圆周角定理得∠ABC=∠ADC,于是得证∠ABC=∠F;
(2)连接BD.由直径所对的圆周角是直角得∠ADB=90°,因为∠ABF=90°,所以∠A=∠DBF,于是得∠C=∠DBF.在Rt△DBF中得BD=8.在Rt△ABD中,sinC=sinA=
,AB=
,于是⊙O的半径为
.
(2)连接BD.由直径所对的圆周角是直角得∠ADB=90°,因为∠ABF=90°,所以∠A=∠DBF,于是得∠C=∠DBF.在Rt△DBF中得BD=8.在Rt△ABD中,sinC=sinA=
| 3 |
| 5 |
| 40 |
| 3 |
| 20 |
| 3 |
解答:(1)证明:∵BF为⊙O的切线,
∴AB⊥BF于点B.
∵CD⊥AB,
∴∠ABF=∠AHD=90°.
∴CD∥BF.
∴∠ADC=∠F.
又∵∠ABC=∠ADC,
∴∠ABC=∠F.
(2)解:连接BD.
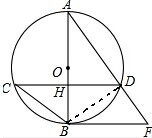
∵AB为⊙O的直径,
∴∠ADB=90°,
由(1)∠ABF=90°,
∴∠A=∠DBF.
又∵∠A=∠C.
∴∠C=∠DBF.
在Rt△DBF中,sinC=sin∠DBF=
,DF=6,
∴BD=8.
在Rt△ABD中,sinC=sinA=
,
∴AB=
.
∴⊙O的半径为
.
∴AB⊥BF于点B.
∵CD⊥AB,
∴∠ABF=∠AHD=90°.
∴CD∥BF.
∴∠ADC=∠F.
又∵∠ABC=∠ADC,
∴∠ABC=∠F.
(2)解:连接BD.

∵AB为⊙O的直径,
∴∠ADB=90°,
由(1)∠ABF=90°,
∴∠A=∠DBF.
又∵∠A=∠C.
∴∠C=∠DBF.
在Rt△DBF中,sinC=sin∠DBF=
| 3 |
| 5 |
∴BD=8.
在Rt△ABD中,sinC=sinA=
| 3 |
| 5 |
∴AB=
| 40 |
| 3 |
∴⊙O的半径为
| 20 |
| 3 |
点评:本题主要考查了切线的性质以及解直角三角形,还用到圆周角定理及其推论,运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
在平行四边形ABCD中,对角线AC、BD相交于点O,如果AC=10,BD=8,AB=x,则x的取值范围是( )
| A、1<x<9 |
| B、2<x<18 |
| C、8<x<10 |
| D、4<x<5 |
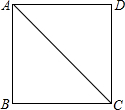 如图,在正方形ABCD中,对角线AC为2,则正方形边长为
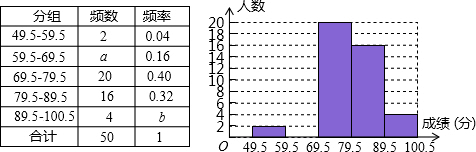
如图,在正方形ABCD中,对角线AC为2,则正方形边长为 高老师将九(1)班某次数学测验成绩分成0~25、26~50、51~75、76~100四组,制作了如下统计表:
高老师将九(1)班某次数学测验成绩分成0~25、26~50、51~75、76~100四组,制作了如下统计表: