题目内容
14．
如图，?ABCD的周长是26cm，对角线AC与BD交于点O，AC⊥AB，点E是BC的中点，△AOD的周长比△AOB的周长多3cm，则AE的长度为4cm．
分析 由?ABCD的周长为26cm，对角线AC、BD相交于点O，若△AOD的周长比△AOB的周长多3cm，可得AB+AD=13cm，AD-AB=3cm，求出AB和AD的长，得出BC的长，再由直角三角形斜边上的中线性质即可求得答案．
解答 解：∵?ABCD的周长为26cm，
∴AB+AD=13cm，OB=OD，
∵△AOD的周长比△AOB的周长多3cm，
∴（OA+OD+AD）-（OA+OB+AB）=AD-AB=3cm，
∴AB=5cm，AD=8cm．
∴BC=AD=8cm．
∵AC⊥AB，E是BC中点，
∴AE=$\frac{1}{2}$BC=4cm；
故答案为：4．
点评 此题考查了平行四边形的性质、直角三角形斜边上的中线性质．熟练掌握平行四边形的性质，由直角三角形斜边上的中线性质求出AE是解决问题的关键．
练习册系列答案
阅读快车系列答案
相关题目
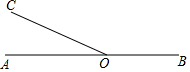在直线AB上任取一点O，过点O作射线OC、OD，使OC⊥OD，如果∠AOC=30°，OE平分∠BOD，求∠COE（要求：将图形补充完整，写出求解过程）
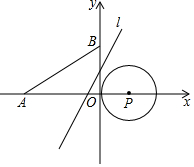如图，平面直角坐标系中，点P的坐标为（1，0），⊙P的半径为1，点A的坐标为（-3，0），点B在y轴的正半轴上，且OB=$\sqrt{3}$．若直线1：y=$\sqrt{3}$x+m从点B开始沿y轴向下平移，线段AB与线段A′B′关于直线1对称．若线段A′B′与⊙P只有一个公共点，则m的值为$\sqrt{3}$或-$\frac{\sqrt{3}}{3}$．
2．下列计算正确的是（ ）
| A． | 3m+2y=5my | B． | 3a2+2a3=5a5 | C． | 4a2-3a2=1 | D． | -2ba2+a2b=-a2b |
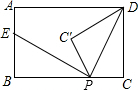如图，在矩形ABCD中，AB=3，BC=5，点P是BC边上的一个动点（点P不与点B、C重合），现将△PCD沿直线PD折叠，使点C落在点C’处，作么BPC'的角平分线交AB于点E．设BP=x，BE=y，给出如下结论：
△ABC中，AB=AC，D为AC上一点（不与A，C重合），
如图点B、D在线段AE上，BC∥EF，AD=BE，BC=EF，