题目内容
18.已知$\left\{\begin{array}{l}{x=3}\\{y=-2}\end{array}\right.$与$\left\{\begin{array}{l}{x=-1}\\{y=6}\end{array}\right.$都是方程ax-y+b=0的解.(1)求a、b的值‘
(2)若y的值不小于0,求x的取值范围
(3)若-2≤x<4,求y的取值范围.
分析 (1)把$\left\{\begin{array}{l}{x=3}\\{y=-2}\end{array}\right.$与$\left\{\begin{array}{l}{x=-1}\\{y=6}\end{array}\right.$代入方程即可得到一个关于a、b的方程组即可求解.
(2)由(1)得y=-2x+4,根据题意得出-2x+4≥0,解不等式,即可求得;
(3)由-2x-y+4=0得x=-$\frac{1}{2}$y+2,根据题意得出$\left\{\begin{array}{l}{-\frac{1}{2}y+2≥-2}\\{-\frac{1}{2}y+2<4}\end{array}\right.$,解不等式组,即可求得.
解答 解:(1)根据题意得:$\left\{\begin{array}{l}{3a+2+b=0}\\{-a-6+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-2}\\{b=4}\end{array}\right.$.
(2)由(1)得方程为-2x-y+4=0,
∴y=-2x+4,
∵y≥0,
∴-2x+4≥0,
解得x≤2;
(3)∵-2x-y+4=0,
∴x=-$\frac{1}{2}$y+2,
∵-2≤x<4,
∴$\left\{\begin{array}{l}{-\frac{1}{2}y+2≥-2}\\{-\frac{1}{2}y+2<4}\end{array}\right.$,
解得-4<y≤8.
点评 本题考查了二元一次方程组的解以及解不等式(组),根据题意得出不等式(组)是解题的关键.

练习册系列答案
相关题目
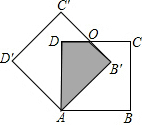 如图,边长为1的正方形ABCD中绕点A逆时针旋转30°得到正方形AB′C′D′,则图中阴影部分的面积为$\frac{{\sqrt{3}}}{3}$.
如图,边长为1的正方形ABCD中绕点A逆时针旋转30°得到正方形AB′C′D′,则图中阴影部分的面积为$\frac{{\sqrt{3}}}{3}$.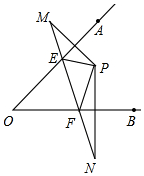 如图,点P在∠AOB内,点M、N分别是P点关于OA、OB的对称点,且MN交OA、OB相交于点E,若△PEF的周长为20,求MN的长.
如图,点P在∠AOB内,点M、N分别是P点关于OA、OB的对称点,且MN交OA、OB相交于点E,若△PEF的周长为20,求MN的长.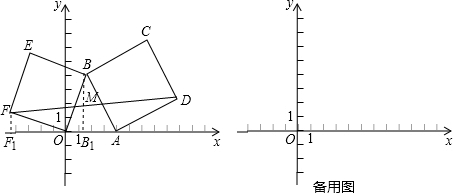
 (1)解一元一次方程:2(0.1x-2)=2.2x+3;
(1)解一元一次方程:2(0.1x-2)=2.2x+3;