题目内容
某儿童商店欲购进一批甲、乙两种新型玩具,甲种玩具每个进价300元,乙种玩具每个进价150元,该店计划用不低于6000元且不高于6450元的资金购进30个甲、乙两种玩具.
(1)求该店购进这两种玩具,共有哪几中购买方案;
(2)若该商店以甲种每个420元,乙种每个225元的价格全部出售,哪种方案获利最大?最大利润是多少元?
(1)求该店购进这两种玩具,共有哪几中购买方案;
(2)若该商店以甲种每个420元,乙种每个225元的价格全部出售,哪种方案获利最大?最大利润是多少元?
考点:一次函数的应用,一元一次不等式组的应用
专题:
分析:(1)根据用不低于6000元且不高于6450元的资金购进30个甲、乙两种玩具,可得一元一次不等式组,解一元一次不等式组,可得答案;
(2)根据利润关系,可得一次函数,根据k的值,函数的性质,可得答案.
(2)根据利润关系,可得一次函数,根据k的值,函数的性质,可得答案.
解答:解:设该商店购进甲种玩具x个,则购进乙种玩具(30-x)个,由题意得,
解这个不等式组,得10≤x≤13,
∵x为整数,
∴x取10,11,12,13
∴30-x取20,19,18,17
答:方案①购进甲种10个,乙种20个;②购进甲种11个,乙种19个;③购进甲种12个,乙种18个;④购进甲种13个,乙种17个;
(2)设该店全部出售甲、乙两种玩具后获利y元,
则y=(420-300)x+(225-150)(30-x)
=120x+2250-75x=45x+2250.
∵45>0,
∴y随x增大而增大,
∴当x=13时,y最大.
∴方案④即购进甲种13个,乙款17个,获利最大.
答:购进甲种13个,乙款17个,获利最大.
|
解这个不等式组,得10≤x≤13,
∵x为整数,
∴x取10,11,12,13
∴30-x取20,19,18,17
答:方案①购进甲种10个,乙种20个;②购进甲种11个,乙种19个;③购进甲种12个,乙种18个;④购进甲种13个,乙种17个;
(2)设该店全部出售甲、乙两种玩具后获利y元,
则y=(420-300)x+(225-150)(30-x)
=120x+2250-75x=45x+2250.
∵45>0,
∴y随x增大而增大,
∴当x=13时,y最大.
∴方案④即购进甲种13个,乙款17个,获利最大.
答:购进甲种13个,乙款17个,获利最大.
点评:本题主要考查了一次函数的应用,(1)列不等式组是解题关键,(2)一次函数的性质是解题关键,注意x只能取10,11,12,13.

练习册系列答案
相关题目
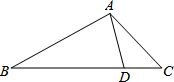 如图,在△ABC中,AC=4,AB=6,BC=8,点D在BC边上,且CD=2,则AD的长为
如图,在△ABC中,AC=4,AB=6,BC=8,点D在BC边上,且CD=2,则AD的长为 数):
数):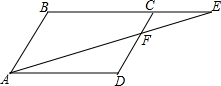 如图,四边形ABCD为?,BC=2CE,则S△CEF:S四边形ABCD=
如图,四边形ABCD为?,BC=2CE,则S△CEF:S四边形ABCD=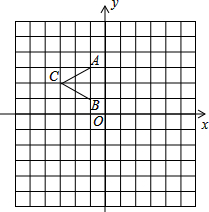 如图,△ABC三个顶点坐标分别为A(-1,3),B(-1,1),C(-3,2)
如图,△ABC三个顶点坐标分别为A(-1,3),B(-1,1),C(-3,2)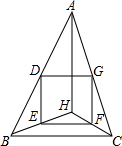 如图,锐角△ABC中,点H是三条高的交点,点D、E、F、G分别是AB、BH、CH、AC的中点.
如图,锐角△ABC中,点H是三条高的交点,点D、E、F、G分别是AB、BH、CH、AC的中点.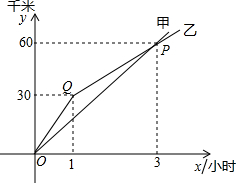 自行车运动员甲、乙在公路上进行训练.如图,是反映他们在训练过程中的行驶路程(千米)和行驶时间(小时)之间的部分图象.
自行车运动员甲、乙在公路上进行训练.如图,是反映他们在训练过程中的行驶路程(千米)和行驶时间(小时)之间的部分图象.