题目内容
17．先化简，再求值：（1-$\frac{1}{x+2}$）÷$\frac{{x}^{2}+2x+1}{x+2}$，其中x=$\sqrt{2}$-1．分析 先根据分式混合元算的法则把原式进行化简，再代入进行计算即可．
解答 解：原式=$\frac{x-1}{x-2}$•$\frac{x+2}{（x+1）^{2}}$
=$\frac{1}{x-1}$，
当x=$\sqrt{2}$-1时，原式=$\frac{\sqrt{2}}{2}$
点评 本题考查了分式的化简求值．解题的关键是对分式的分子分母要因式分解．
练习册系列答案
尖子生新课堂课时作业系列答案
英才计划同步课时高效训练系列答案
相关题目
7．在Rt△ABC中，∠C=90°，若tanA=$\frac{5}{12}$，则sinA=（ ）
| A． | $\frac{12}{13}$ | B． | $\frac{5}{12}$ | C． | $\frac{13}{5}$ | D． | $\frac{5}{13}$ |
一艘轮船位于灯塔P南偏西60°方向上的点A处，在A正东方向上距离20海里的有一点B处，在灯塔P南偏西45°方向上，求A距离灯塔P的距离．
在数学课上，老师提出如下问题：
9．折纸探究tan 22.5°的值：如图①，矩形纸片ABCD（AD＞AB）中，AB=1，将矩形纸片ABCD沿折痕AE对折，使B点落在边AD上，点B和点F重合，如图②所示；再剪去四边形CEFD，余下部分如图③所示；将图③中的纸片沿折痕AG对折，使点F落在AE边的点H处，如图④所示．则tan 22.5°的值为（ ）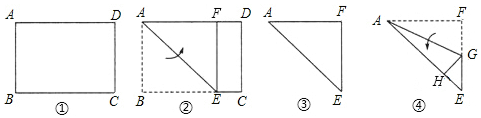
| A． | $\sqrt{2}$-1 | B． | $\sqrt{2}$+1 | C． | $\frac{2}{3}$ | D． | $\frac{\sqrt{2}+1}{2}$ |