题目内容
6.某商店第一次用300元购进笔记本若干,第二次又用300元购进该款笔记本,但这次每本的进价是第一次进价的$\frac{4}{3}$倍,购进数量比第一次少了25本.(1)求第一次每本笔记本的进价是多少元?
(2)若要求这两次购进的笔记本按同一价格全部销售完毕后获利不低于450元,问每本笔记本的售价至少是多少元?
分析 (1)设第一次每本笔记本的进价是x元,则第二次每本笔记本的进价是$\frac{4}{3}$x元,根据数量=总价÷单价结合第二次比第一次少购进25本,即可得出关于x的分式方程,解之并检验后即可得出结论;
(2)根据数量=总价÷单价求出第一次购进笔记本的数量,结合一、二次购进笔记本数量间的关系求出两次共购进的本数,设每本笔记本的售价是y元,根据利润=销售单价×销售数量-进价,即可得出关于y的一元一次不等式,解之即可得出y的取值范围,取其内的最小值即可得出结论.
解答 解:(1)设第一次每本笔记本的进价是x元,则第二次每本笔记本的进价是$\frac{4}{3}$x元,
根据题意得:$\frac{300}{x}$-$\frac{300}{\frac{4}{3}x}$=25,
解得:x=3,
经检验,x=3是原方程的解,且符合题意.
答:第一次每本笔记本的进价是3元.
(2)300÷3=100(本),
100-25+100=175(本).
设每本笔记本的售价是y元,
根据题意得:175y-300-300≥450,
解得:y≥6.
答:每本笔记本的售价至少是6元.
点评 本题考查了分式方程的应用以及一元一次不等式的应用,解题的关键是:(1)根据数量=总价÷单价结合第二次比第一次少购进25本,列出关于x的分式方程;(2)根据利润=销售单价×销售数量-进价,列出关于y的一元一次不等式.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
1.下列说法正确的是( )
| A. | 为了解苏州市中学生的睡眠情况,应该采用普查的方式 | |
| B. | 某种彩票的中奖机会是1%,则买100张这种彩票一定会中奖 | |
| C. | 一组数据1,5,3,2,3,4,8的众数和中位数都是3 | |
| D. | 若甲组数据的方差s甲2=0.1,乙组数据的方差s乙2=0.2,则乙组数据比甲组数据稳定 |
16.平面直角坐标系中,点P的坐标为(3,3),将抛物线y=-$\frac{1}{2}$x2+2x+3沿水平方向或竖直方向平移,使其经过点P,则平移的最短距离为( )
| A. | 1 | B. | $\frac{3}{2}$ | C. | $\sqrt{5}$ | D. | 3 |
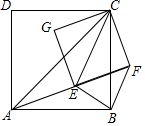 如图,四边形ABCD,和四边形CFEG都是正方形,连接AC、AE、BF、CE.
如图,四边形ABCD,和四边形CFEG都是正方形,连接AC、AE、BF、CE.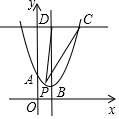 如图,在平面直角坐标系中,点A在y轴上,点A、B($\frac{3}{2}$,m)、C(3,n)均在抛物线y=(x-1)2+1上,点D在抛物线的对称轴上,CD∥x轴.若点P为抛物线上A、B两点间任意一点(包括点A、B),则△PCD面积S的取值范围是3≤S≤$\frac{15}{4}$.
如图,在平面直角坐标系中,点A在y轴上,点A、B($\frac{3}{2}$,m)、C(3,n)均在抛物线y=(x-1)2+1上,点D在抛物线的对称轴上,CD∥x轴.若点P为抛物线上A、B两点间任意一点(包括点A、B),则△PCD面积S的取值范围是3≤S≤$\frac{15}{4}$.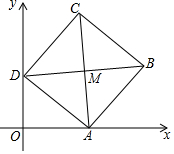 在平面直角坐标系中,正方形ABCD的顶点A,D分别在x轴、y轴正半轴上,AC,BD交于点M,若OA=8,OD=6,则点M的坐标为(7,7).
在平面直角坐标系中,正方形ABCD的顶点A,D分别在x轴、y轴正半轴上,AC,BD交于点M,若OA=8,OD=6,则点M的坐标为(7,7).