题目内容
9.折纸探究tan 22.5°的值:如图①,矩形纸片ABCD(AD>AB)中,AB=1,将矩形纸片ABCD沿折痕AE对折,使B点落在边AD上,点B和点F重合,如图②所示;再剪去四边形CEFD,余下部分如图③所示;将图③中的纸片沿折痕AG对折,使点F落在AE边的点H处,如图④所示.则tan 22.5°的值为( )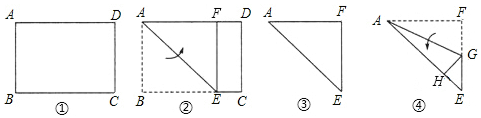
| A. | $\sqrt{2}$-1 | B. | $\sqrt{2}$+1 | C. | $\frac{2}{3}$ | D. | $\frac{\sqrt{2}+1}{2}$ |
分析 设FG=x,则GH=x,根据△EHG是等腰直角三角形,可得GE=$\sqrt{2}$GH=$\sqrt{2}$x,根据EF=1,可得x+$\sqrt{2}$x=1,进而得到x=$\sqrt{2}$-1,即FG=$\sqrt{2}$-1,在Rt△AFG中,根据tan∠FAG=tan22.5°=$\frac{FG}{AF}$进行计算即可.
解答  解:如图④,设FG=x,则GH=x,
解:如图④,设FG=x,则GH=x,
由折叠可得,∠GHE=90°,∠GEH=45°,
∴△EHG是等腰直角三角形,
∴GE=$\sqrt{2}$GH=$\sqrt{2}$x,
∵图②中,∠B=∠BAE=∠AFE=90°,AB=BE,
∴四边形ABEF是正方形,
∴EF=AB=AF=1,
∴x+$\sqrt{2}$x=1,
解得x=$\sqrt{2}$-1,
即FG=$\sqrt{2}$-1,
由折叠可得,∠FAG=$\frac{1}{2}$∠EAF=$\frac{1}{4}$∠BAD=22.5°,
∴Rt△AFG中,tan∠FAG=tan22.5°=$\frac{FG}{AF}$=$\frac{\sqrt{2}-1}{1}$=$\sqrt{2}-1$,
故选:A.
点评 本题主要考查了折叠问题,正方形的性质以及等腰直角三角形的性质的运用,解决问题的关键是依据等量关系列方程求解.折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,对应边和对应角相等.

练习册系列答案
相关题目
19.化简$\frac{4}{x-4}$+$\frac{x}{4-x}$的结果是( )
| A. | -1 | B. | 1 | C. | -3 | D. | 3 |
1.下列说法正确的是( )
| A. | 为了解苏州市中学生的睡眠情况,应该采用普查的方式 | |
| B. | 某种彩票的中奖机会是1%,则买100张这种彩票一定会中奖 | |
| C. | 一组数据1,5,3,2,3,4,8的众数和中位数都是3 | |
| D. | 若甲组数据的方差s甲2=0.1,乙组数据的方差s乙2=0.2,则乙组数据比甲组数据稳定 |
19.某校组织九年级学生参加中考体育测试,共租3辆客车,分别编号为1、2、3,李军和赵娟两人可任选一辆车乘坐,则两人同坐一辆车的概率为( )
| A. | $\frac{1}{9}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
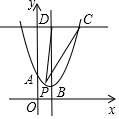 如图,在平面直角坐标系中,点A在y轴上,点A、B($\frac{3}{2}$,m)、C(3,n)均在抛物线y=(x-1)2+1上,点D在抛物线的对称轴上,CD∥x轴.若点P为抛物线上A、B两点间任意一点(包括点A、B),则△PCD面积S的取值范围是3≤S≤$\frac{15}{4}$.
如图,在平面直角坐标系中,点A在y轴上,点A、B($\frac{3}{2}$,m)、C(3,n)均在抛物线y=(x-1)2+1上,点D在抛物线的对称轴上,CD∥x轴.若点P为抛物线上A、B两点间任意一点(包括点A、B),则△PCD面积S的取值范围是3≤S≤$\frac{15}{4}$.