题目内容
7.在Rt△ABC中,∠C=90°,若tanA=$\frac{5}{12}$,则sinA=( )| A. | $\frac{12}{13}$ | B. | $\frac{5}{12}$ | C. | $\frac{13}{5}$ | D. | $\frac{5}{13}$ |
分析 先利用正切的定义得到tanA=$\frac{BC}{AC}$=$\frac{5}{12}$,则设BC=5x,AC=12x,利用勾股定理计算出AB=13x,然后根据正弦的定义求解.
解答 解:∵∠C=90°,
∴tanA=$\frac{BC}{AC}$=$\frac{5}{12}$,
设BC=5x,AC=12x,
∴AB=$\sqrt{(5x)^{2}+(12x)^{2}}$=13x,
∴sinA=$\frac{BC}{AB}$=$\frac{5x}{13x}$=$\frac{5}{13}$.
故选D.
点评 本题考查了同角三角函数的关系:正余弦与正切之间的关系(积的关系):一个角的正切值等于这个角的正弦与余弦的比.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.下列方程的变形正确的是( )
| A. | 由2x-3=4x,得:2x=4x-3 | B. | 由7x-4=3-2x,得:7x+2x=3-4 | ||
| C. | 由$\frac{1}{3}$x-$\frac{1}{2}$=3x+4得-$\frac{1}{2}$-4=3x+$\frac{1}{3}$x | D. | 由3x-4=7x+5得:3x-7x=5+4 |
19.化简$\frac{4}{x-4}$+$\frac{x}{4-x}$的结果是( )
| A. | -1 | B. | 1 | C. | -3 | D. | 3 |
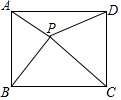 如图,点P是矩形ABCD内一点,连接PA、PB、PC、PD,已知AB=3,BC=4,设△PAB、△PBC、△PDA的面积分别为S1、S2、S3、S4,以下判断:
如图,点P是矩形ABCD内一点,连接PA、PB、PC、PD,已知AB=3,BC=4,设△PAB、△PBC、△PDA的面积分别为S1、S2、S3、S4,以下判断:
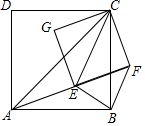 如图,四边形ABCD,和四边形CFEG都是正方形,连接AC、AE、BF、CE.
如图,四边形ABCD,和四边形CFEG都是正方形,连接AC、AE、BF、CE.