题目内容
6. 已知点A在反比例函数y=$\frac{3}{x}$的图象上,点B与点A关于原地对称,BC∥y轴,与反比例函数y=-$\frac{2}{x}$的图象交于点C,连接AC,则△ABC的面积为5.
已知点A在反比例函数y=$\frac{3}{x}$的图象上,点B与点A关于原地对称,BC∥y轴,与反比例函数y=-$\frac{2}{x}$的图象交于点C,连接AC,则△ABC的面积为5.
分析 由点A在反比例函数y=$\frac{3}{x}$的图象上,可设点A的坐标为(m,$\frac{3}{m}$),则B(-m,-$\frac{3}{m}$),C(-m,$\frac{2}{m}$),根据三角形的面积公式即可得出S△ABC的值.
解答 解:设点A的坐标为(m,$\frac{3}{m}$),则B(-m,-$\frac{3}{m}$),C(-m,$\frac{2}{m}$),
∴S△ABC=$\frac{1}{2}$BC•(xA-xB)=$\frac{1}{2}$(yC-yB)•(xA-xB)=$\frac{1}{2}$[$\frac{2}{m}$-(-$\frac{3}{m}$)]•[m-(-m)]=$\frac{1}{2}$×$\frac{5}{m}$×2m=5.
故答案为:5.
点评 本题考查了反比例函数图象上点的坐标特征以及三角形的面积,解题的关键是设出点A的坐标,用其表示出点B、C的坐标.本题属于基础题,难度不大,解决该题型题目时,根据反比例函数图象上点的坐标特征表示出三角形的顶点坐标是关键.

练习册系列答案
相关题目
18.|-2015|的值是( )
| A. | $\frac{1}{2015}$ | B. | -$\frac{1}{2015}$ | C. | 2015 | D. | -2015 |
 如图,有两棵树,一棵高7m,另一棵高2m,两树相距12m.一只小鸟从一棵树的树梢(点A)飞到另一棵树的树梢(点C),请问小鸟至少飞行多少米?
如图,有两棵树,一棵高7m,另一棵高2m,两树相距12m.一只小鸟从一棵树的树梢(点A)飞到另一棵树的树梢(点C),请问小鸟至少飞行多少米? 如图,AD∥BC,∠ABC的角平分线BP与∠BAD的角平分线AP相交于点P,作PE⊥AB于点E.若PE=2cm,则两平行线AD与BC间的距离为4 cm.
如图,AD∥BC,∠ABC的角平分线BP与∠BAD的角平分线AP相交于点P,作PE⊥AB于点E.若PE=2cm,则两平行线AD与BC间的距离为4 cm.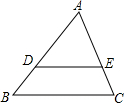 如图,已知D为△ABC边AB上一点,AD=2BD,DE∥BC交AC于E,AE=6,则EC=3.
如图,已知D为△ABC边AB上一点,AD=2BD,DE∥BC交AC于E,AE=6,则EC=3.