题目内容
15.解方程:(1)$\frac{1}{3}$(4-y)=$\frac{1}{4}$(y+3)
(2)$\frac{3y+12}{4}$=2-$\frac{5y-7}{3}$
(3)5-2|$\frac{1}{2}$x-6|=2.
分析 (1)首先方程两边同乘以12,在进行化简,即可求得方程的解;
(2)首先方程两边同乘以12,在进行化简,即可求得方程的解;
(3)先移项,再去绝对值符号,即可求得方程的解.
解答 解:(1)$\frac{1}{3}$(4-y)=$\frac{1}{4}$(y+3)
方程两边同乘以12,得
4(4-y)=3(y+3)
化简,得
7y=7
解得,y=1;
(2)$\frac{3y+12}{4}$=2-$\frac{5y-7}{3}$
方程两边同乘以12,得
3(3y+12)=24-4(5y-7)
化简,得
29y=16
解得,y=$\frac{16}{29}$;
(3)5-2|$\frac{1}{2}$x-6|=2
移项,得
$2|\frac{1}{2}x-6|=3$
$|\frac{1}{2}x-6|=\frac{3}{2}$
则$\frac{1}{2}x-6=\frac{3}{2}或\frac{1}{2}x-6=-\frac{3}{2}$
解得,x=15或x=9.
点评 本题考查解一元一次方程,解题的关键是能去分母的先去分母,注意带绝对值得方程的解法,要分两种情况进行解答.

练习册系列答案
相关题目
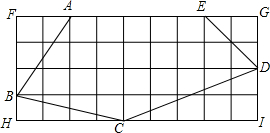 如图,每个小方格都是边长为1的正方形,计算五边形ABCDE的周长.
如图,每个小方格都是边长为1的正方形,计算五边形ABCDE的周长. 如图是一个程序计算器,现输入m=-6,那么输出的结果是25.
如图是一个程序计算器,现输入m=-6,那么输出的结果是25. 如图一根木棒放在数轴上,木棒的左端与数轴上的点A重合,右端与点B重合.
如图一根木棒放在数轴上,木棒的左端与数轴上的点A重合,右端与点B重合. 如图,五边形ABCDE和五边形JFGHI相似,求角α,β的大小和x,y,z的值.
如图,五边形ABCDE和五边形JFGHI相似,求角α,β的大小和x,y,z的值.