题目内容
6.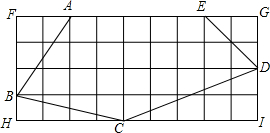 如图,每个小方格都是边长为1的正方形,计算五边形ABCDE的周长.
如图,每个小方格都是边长为1的正方形,计算五边形ABCDE的周长.
分析 根据勾股定理分别计算出五边形ABCDE的各边长,根据周长公式计算即可.
解答 解:AB=$\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{13}$,
BC=$\sqrt{{4}^{2}+{1}^{2}}$=$\sqrt{17}$,
CD=$\sqrt{{5}^{2}+{2}^{2}}$=$\sqrt{29}$,
DE=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
AE=5,
故五边形ABCDE的周长=$\sqrt{13}$+$\sqrt{17}$+$\sqrt{29}$+2$\sqrt{2}$+5.
点评 本题考查的是勾股定理的应用,一个直角三角形中,两条直角边长的平方之和等于斜边长的平方.

练习册系列答案
相关题目
14.已知二次函数函数y=(k-3)x2+2x-1的图象与x轴有交点,则k的取值范围是( )
| A. | k≥2 | B. | k≤2 | C. | k≥2且k≠3 | D. | k≥-4且k≠3 |
18.若x=-1是方程ax2+b=0的一个根,则方程的另一根为( )
| A. | 1 | B. | ±1 | C. | 2 | D. | -2 |
 如图是一次函数y=kx+b的图象,当y>0时,x的取值范围是x<3;y≥3时,x的取值范围是x≤0.
如图是一次函数y=kx+b的图象,当y>0时,x的取值范围是x<3;y≥3时,x的取值范围是x≤0. 如图,直线y=2x与直线y=kx+3交于点A(1,m),直线y=kx+3分别与y轴、x轴交于点B,C
如图,直线y=2x与直线y=kx+3交于点A(1,m),直线y=kx+3分别与y轴、x轴交于点B,C