题目内容
7. 如图,?ABCD中AD=2AB,CE平分∠BCD交AD边于点E,且AE=4,则AB的长为4.
如图,?ABCD中AD=2AB,CE平分∠BCD交AD边于点E,且AE=4,则AB的长为4.
分析 根据平行四边形性质得出AB=DC,AD∥BC,推出∠DEC=∠BCE,求出∠DEC=∠DCE,推出DE=DC=AB,得出AD=2DE即可.
解答 解:∵四边形ABCD是平行四边形,
∴AB=DC,AD∥BC,
∴∠DEC=∠BCE,
∵CE平分∠DCB,
∴∠DCE=∠BCE,
∴∠DEC=∠DCE,
∴DE=DC=AB,
∵AD=2AB=2CD,CD=DE,
∴AD=2DE,
∴AE=DE=4,
∴DC=AB=DE=4,
故答案为4.
点评 本题考查了平行四边形性质,平行线性质,角平分线定义,等腰三角形的性质和判定的应用,关键是求出DE=AE=DC.

练习册系列答案
相关题目
17. 如图,⊙O的半径长6cm,点C在⊙O上,弦AB垂直平分OC于点D,则弦AB的长为( )
如图,⊙O的半径长6cm,点C在⊙O上,弦AB垂直平分OC于点D,则弦AB的长为( )
 如图,⊙O的半径长6cm,点C在⊙O上,弦AB垂直平分OC于点D,则弦AB的长为( )
如图,⊙O的半径长6cm,点C在⊙O上,弦AB垂直平分OC于点D,则弦AB的长为( )| A. | 9cm | B. | $6\sqrt{3}$cm | C. | $\frac{9}{2}$cm | D. | $3\sqrt{3}$cm |
18.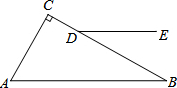 如图,在△ABC中,∠C=90°,点D在BC边上,DE∥AB,若∠CDE=150°,则∠A的度数为( )
如图,在△ABC中,∠C=90°,点D在BC边上,DE∥AB,若∠CDE=150°,则∠A的度数为( )
 如图,在△ABC中,∠C=90°,点D在BC边上,DE∥AB,若∠CDE=150°,则∠A的度数为( )
如图,在△ABC中,∠C=90°,点D在BC边上,DE∥AB,若∠CDE=150°,则∠A的度数为( )| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
2.已知一组数据:15,13,15,16,17,16,14,15,则这组数据的众数和中位数分别是( )
| A. | 15,15 | B. | 15,14 | C. | 16,14 | D. | 16,15 |
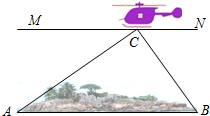 如图,为了开发利用海洋资源,我勘测飞机测量钓鱼岛附属岛屿之一的北小岛(又称为鸟岛)两侧端点A、B的距离,飞机在距海平面垂直高度为100米的北小岛上方点C处测得端点A的俯角为30°,测得端点B的俯角为45°,求北小岛两侧端点A、B的距离.
如图,为了开发利用海洋资源,我勘测飞机测量钓鱼岛附属岛屿之一的北小岛(又称为鸟岛)两侧端点A、B的距离,飞机在距海平面垂直高度为100米的北小岛上方点C处测得端点A的俯角为30°,测得端点B的俯角为45°,求北小岛两侧端点A、B的距离.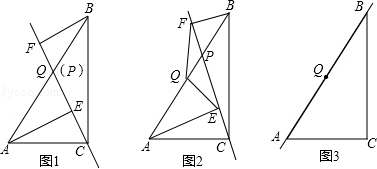
 如图,在⊙O中,∠AOB=150°,∠ABC=45°,延长OB到D,使BD=OB,连接CD.
如图,在⊙O中,∠AOB=150°,∠ABC=45°,延长OB到D,使BD=OB,连接CD.