题目内容
9.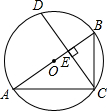 如图,⊙O的直径AB垂直于弦CD,垂足为E.若∠B=60°,AC=3,则CD的长为( )
如图,⊙O的直径AB垂直于弦CD,垂足为E.若∠B=60°,AC=3,则CD的长为( )| A. | 6 | B. | $2\sqrt{3}$ | C. | $\sqrt{3}$ | D. | 3 |
分析 由AB是⊙O的直径,根据直径所对的圆周角是直角,可求得∠ACB=90°,又由∠B=60°,AC=3,即可求得BC的长,然后由AB⊥CD,可求得CE的长,又由垂径定理,求得答案.
解答 解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠B=60°,AC=3,
∴BC=$\frac{AC}{tan60°}$=$\sqrt{3}$,
∵AB⊥CD,
∴CE=BC•sin60°=$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=$\frac{3}{2}$,
∴CD=2CE=3.
故选D.
点评 此题考查了圆周角定理、垂径定理以及三角函数的性质.注意直径所对的圆周角是直角,得到∠ACD=90°是关键.

练习册系列答案
相关题目
20.在同一个平面内,不重合的两条直线的位置关系是( )
| A. | 平行 | B. | 相交 | C. | 平行或相交 | D. | 无法确定 |
17. 如图,⊙O的半径长6cm,点C在⊙O上,弦AB垂直平分OC于点D,则弦AB的长为( )
如图,⊙O的半径长6cm,点C在⊙O上,弦AB垂直平分OC于点D,则弦AB的长为( )
 如图,⊙O的半径长6cm,点C在⊙O上,弦AB垂直平分OC于点D,则弦AB的长为( )
如图,⊙O的半径长6cm,点C在⊙O上,弦AB垂直平分OC于点D,则弦AB的长为( )| A. | 9cm | B. | $6\sqrt{3}$cm | C. | $\frac{9}{2}$cm | D. | $3\sqrt{3}$cm |
4.2015年北京市实施能源清洁化战略,全市燃煤总量减少到15 000万吨左右,将15 000用科学记数法表示应为( )
| A. | 0.15×105 | B. | 1.5×104 | C. | 1.5×105 | D. | 15×103 |
1.随着人们生活质量的提高,净水器已经慢慢走入了普通百姓家庭,某电器公司销售每台进价分别为2000元、1700元的A、B两种型号的净水器,下表是近两周的销售情况:
(1)求A,B两种型号的净水器的销售单价;
(2)若电器公司准备用不多于54000元的金额在采购这两种型号的净水器共30台,求A种型号的净水器最多能采购多少台?
(3)在(2)的条件下,公司销售完这30台净水器能否实现利润为12800元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
| 销售时段 | 销售数量 | 销售收入 | |
| A种型号 | B种型号 | ||
| 第一周 | 3台 | 5台 | 18000元 |
| 第二周 | 4台 | 10台 | 31000元 |
(2)若电器公司准备用不多于54000元的金额在采购这两种型号的净水器共30台,求A种型号的净水器最多能采购多少台?
(3)在(2)的条件下,公司销售完这30台净水器能否实现利润为12800元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
18.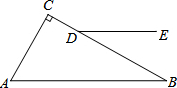 如图,在△ABC中,∠C=90°,点D在BC边上,DE∥AB,若∠CDE=150°,则∠A的度数为( )
如图,在△ABC中,∠C=90°,点D在BC边上,DE∥AB,若∠CDE=150°,则∠A的度数为( )
 如图,在△ABC中,∠C=90°,点D在BC边上,DE∥AB,若∠CDE=150°,则∠A的度数为( )
如图,在△ABC中,∠C=90°,点D在BC边上,DE∥AB,若∠CDE=150°,则∠A的度数为( )| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
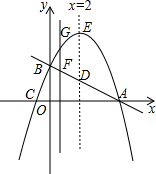 如图,已知直线y=-$\frac{1}{2}$x+2与坐标轴交于A、B两点,抛物线y=-x2+bx+c与x轴交于A、C两点,与y轴交于点B.
如图,已知直线y=-$\frac{1}{2}$x+2与坐标轴交于A、B两点,抛物线y=-x2+bx+c与x轴交于A、C两点,与y轴交于点B.