题目内容
13．
如图所示，长方形OABC的顶点B的坐标为 （4，2），把长方形OABC沿x轴向右平移3cm得到长方形DEFG，则AF=7cm，EB=1cm．
分析 首先根据矩形的性质得出AB=4．再根据平移的性质得出EF=AB=4，BF=AE=3，那么AF=AE+EF=7，EB=AB-AE=1．
解答 解：∵长方形OABC的顶点B的坐标为 （4，2），
∴AB=4．
把长方形OABC沿x轴向右平移3cm得到长方形DEFG，
∴EF=AB=4，BF=AE=3，
∴AF=AE+EF=3+4=7，EB=AB-AE=4-3=1．
故答案为7，1．
点评 本题考查了坐标与图形变化-平移，矩形的性质，根据平移的性质得出EF=AB=4，BF=AE=3是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
如图，∠ABC=90°，∠BCD=120°，∠CDE=30°，试说明AB∥DE．
1．下列计算正确的是（ ）
| A． | $\sqrt{2}$+2=2$\sqrt{2}$ | B． | $\sqrt{4+9}$=$\sqrt{4}$+$\sqrt{9}$ | C． | $\sqrt{4\frac{1}{9}}$=2$\frac{1}{3}$ | D． | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$ |
如图，在?ABCD中，E、F分别是AD、DC的中点，若△CEF的面积为3，则?ABCD的面积为24．
2．在下列所给的条件中，能组成三角形的是（ ）
| A． | 三条线段的比为2：3：4 | B． | 三条线段的比为1：2：3 | ||
| C． | 三条线段的比为4：5：9 | D． | 三条线段的比为7：4：3 |
3．
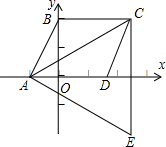如图，△ACE是以?ABCD的对角线AC为边的等边三角形，点C与点E关于x轴对称，若E点的坐标是（5，-2$\sqrt{3}$），则D点的坐标是（ ）
如图，△ACE是以?ABCD的对角线AC为边的等边三角形，点C与点E关于x轴对称，若E点的坐标是（5，-2$\sqrt{3}$），则D点的坐标是（ ）| A． | （3，0） | B． | （4，0） | C． | （5，0） | D． | （2$\sqrt{3}$，0） |