Question

3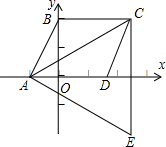．如图，△ACE是以?ABCD的对角线AC为边的等边三角形，点C与点E关于x轴对称，若E点的坐标是（5，-2$\sqrt{3}$），则D点的坐标是（　　）

• A． （3，0）
• B． （4，0）
• C． （5，0）
• D． （2$\sqrt{3}$，0）

Answer 1

分析 首先设CE交x轴于点F，由点C与点E关于x轴对称．若点E的坐标是（5，2$\sqrt{3}$），可求得点C的坐标，继而求得AC与BC的长，然后由三角函数的性质，求得AF的长，即可求得点A的坐标，继而求得答案．

解答 解：设CE交x轴于点F，如图所示：
∵点C与点E关于x轴对称，点E的坐标是（5，-2$\sqrt{3}$），
∴点C的坐标是（5，2$\sqrt{3}$），
∴AC=CE=4$\sqrt{3}$，OF=5，
∵AD∥BC，
∴点B（0，2$\sqrt{3}$），
∵△ACE是等边三角形，AD⊥CE，
∴∠CAD=30°，
∴AF=AC•cos30°=4$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=6，
∴OA=AF-OF=1，
∴点A（-1，0），
∵AD=BC=5，
∴点C的坐标为：（4，0）．
故选：B．

点评 此题考查了平行四边形的性质、等边三角形的性质以及点与坐标的性质．注意掌握平行四边形的对边平行且相等．