题目内容
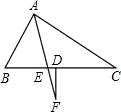 如图,AF平分∠BAC,FD⊥BD.
如图,AF平分∠BAC,FD⊥BD.(1)若∠B-∠C=20°,求∠F度数;
(2)若∠BAC=120°,点D为BC中点,过F分别作FG⊥AB,FH⊥AC,画出图形并求证:AB+AC=AF.
考点:全等三角形的判定与性质,角平分线的性质,线段垂直平分线的性质
专题:
分析:(1)根据AF平分∠BAC,即可求得∠AEC=100°、∠AEB=80°,即可求得∠F的值;
(2)连接BF,CF,根据30°角所对直角边是斜边长一半即可求得AF=AG+AH,在RT△BFG≌RT△CFH可得BG=CH,即可解题.
(2)连接BF,CF,根据30°角所对直角边是斜边长一半即可求得AF=AG+AH,在RT△BFG≌RT△CFH可得BG=CH,即可解题.
解答:解:(1)∵AF平分∠BAC,∠B-∠C=20°,
∴∠AEC-∠AEB=20°,
∵∠AEC+∠AEB=180°,
∴∠AEC=100°,∠AEB=80°,
∴∠F=90°-∠DEF=90°-∠AEB=10°;
(2)连接BF,CF

∵∠BAC=120°,AF为∠BAC平分线
∴∠BAF=60°,BF=FH
∵FG⊥AG,
∴AF=2AG,
同理可证AF=2AH,
∴AF=AG+AH,
∵FD⊥BC,D为BC中点,
∴BF=CF,
在RT△BFG和RT△CFH中,
,
∴RT△BFG≌RT△CFH(HL),
∴BG=CH,
∴AF=AH+AG=AB+BG+AC-CH=AB+AC.
∴∠AEC-∠AEB=20°,
∵∠AEC+∠AEB=180°,
∴∠AEC=100°,∠AEB=80°,
∴∠F=90°-∠DEF=90°-∠AEB=10°;
(2)连接BF,CF

∵∠BAC=120°,AF为∠BAC平分线
∴∠BAF=60°,BF=FH
∵FG⊥AG,
∴AF=2AG,
同理可证AF=2AH,
∴AF=AG+AH,
∵FD⊥BC,D为BC中点,
∴BF=CF,
在RT△BFG和RT△CFH中,
|
∴RT△BFG≌RT△CFH(HL),
∴BG=CH,
∴AF=AH+AG=AB+BG+AC-CH=AB+AC.
点评:此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
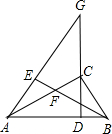 如图,在△ABC中,∠ACB=90°,CD是斜边AB上的高,G是DC延长线上一点,过B作BE⊥AG,垂足为E,交CD于点F.求证:CD2=DF•DG.
如图,在△ABC中,∠ACB=90°,CD是斜边AB上的高,G是DC延长线上一点,过B作BE⊥AG,垂足为E,交CD于点F.求证:CD2=DF•DG.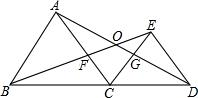 如图△DCE、△ABC均为等边三角形,AD、BE分别交与CE、AC交于点G、F,有下列结论:
如图△DCE、△ABC均为等边三角形,AD、BE分别交与CE、AC交于点G、F,有下列结论: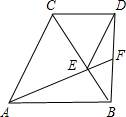 如图,△ABC和△CDE都为等边三角形,E在BC上,AE的延长线交BD于F.
如图,△ABC和△CDE都为等边三角形,E在BC上,AE的延长线交BD于F.