题目内容
已知二次函数y=x2-2x+6,若A(2,y1)、B(2+m,y2)为其图象上的两点,且y1<y2,则实数m的取值范围是 .
考点:二次函数图象上点的坐标特征
专题:
分析:求出二次函数的对称轴,再比较A、B两点的位置,即可得出正确答案.
解答:解:∵函数对称轴为x=-
=1,
∴当y1<y2时,
①B在A的右侧时,2+m>2,m>0;
②B在A的左侧0时,2+m<0,m<-2.
故答案为m>0或m<-2.
| -2 |
| 2×1 |
∴当y1<y2时,
①B在A的右侧时,2+m>2,m>0;
②B在A的左侧0时,2+m<0,m<-2.
故答案为m>0或m<-2.
点评:本题考查了二次函数图象上点的坐标特征,要熟悉二次函数的性质及二次函数的图象.

练习册系列答案
相关题目
下列计算中正确的是( )
| A、6a-5a=1 |
| B、5x-6x=11x |
| C、m2-m=m |
| D、-x3-6x3=-7x3 |
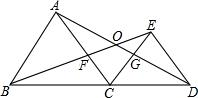 如图△DCE、△ABC均为等边三角形,AD、BE分别交与CE、AC交于点G、F,有下列结论:
如图△DCE、△ABC均为等边三角形,AD、BE分别交与CE、AC交于点G、F,有下列结论: 已知:△ABC中,D为BC边上任意一点,E为AD上任意一点,如图.求证:
已知:△ABC中,D为BC边上任意一点,E为AD上任意一点,如图.求证: 如图,AB是⊙O的直径,
如图,AB是⊙O的直径,
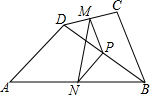 如图,在四边形ABCD中,AD=BC,P是对角线BD的中点,M是DC的中点,N是AB的中点.求证:∠PMN=∠PNM.
如图,在四边形ABCD中,AD=BC,P是对角线BD的中点,M是DC的中点,N是AB的中点.求证:∠PMN=∠PNM.