题目内容
2．先化简，再计算：$\frac{2}{x-2}$-$\frac{8}{{x}^{2}-4}$．其中x=-3．分析 原式化成同分母的分式，然后相减得到最简结果，把x的值代入计算即可求出值．
解答 解：原式=$\frac{2x+4}{（x+2）（x-2）}$-$\frac{8}{（x+2）（x-2）}$
=$\frac{2（x-2）}{（x+2）（x-2）}$
=$\frac{2}{x+2}$，
当x=3时，原式=$\frac{2}{-3+2}$=-2．
点评 此题考查了分式的加减-化简求值，熟练掌握运算法则是解本题的关键．
练习册系列答案
快乐5加2金卷系列答案
相关题目
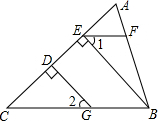如图所示，已知AB⊥BC，GD⊥AC于点D，BE⊥AC于点E，∠1=∠2，判断EF与AB的位置关系，并说明理由．
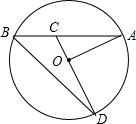如图，已知AB是⊙O的弦，OA=4，∠A=30°，C是弦AB上任意一点（不与点A、B重合），连接CO并延长CO交⊙O于点D，连接BD．
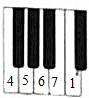如图是钢琴键盘的一部分，若从4开始，依次弹出4，5，6，7，1，4，5，6，7，1，…，按照上述规律弹到第2016个音符是4．
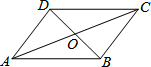如图，在?ABCD中，对角线AC与BD交于点O，∠OBC=90°，AC=6，BD=4，则?ABCD的面积是4$\sqrt{5}$．
7．下列实数中，无理数是（ ）
| A． | $\sqrt{16}$ | B． | 3.14159 | C． | 0 | D． | -$\sqrt{12}$ |
14．函数$y=\sqrt{\frac{1}{2x-1}}$中，自变量x的取值范围是（ ）
| A． | $x＞\frac{1}{2}$ | B． | $x≥\frac{1}{2}$ | C． | $x＜\frac{1}{2}$ | D． | $x≠\frac{1}{2}$ |
11．已知a＞0，b＜0，|a|＜|b|，则（ ）
| A． | a+b＜0 | B． | b-a＞0 | C． | ab＞0 | D． | $\frac{a}{b}$＞0 |
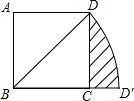如图，在正方形ABCD中，对角线BD的长为$\sqrt{2}$．若将BD绕点B旋转后，点D落在BC延长线上的点D′处，点D经过的路径为弧DD′，则图中阴影部分的面积是$\frac{π}{4}-\frac{1}{2}$．