Question

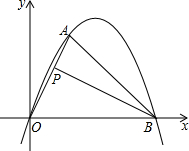在平面直角坐标系中，B（

3

+1，0 ），点A在第一象限内，且∠AOB=60°，∠ABO=45°．
（1）求点A的坐标；
（2）求过A、O、B三点的抛物线解析式；
（3）动点P从O 点出发，以每秒2个单位的速度沿OA运动到点A止，是否存在t，使△POB的外心在x轴上？若不存在，请你说明理由；若存在，请求出t的值．

Answer 1

考点：二次函数综合题

专题：

分析：（1）过点A作AC⊥OB于点C．通过解Rt△AOC和在Rt△ABC可以求得AC=BC=

3

x；然后利用OC+BC=OB列出关于x的方程x+

3

x=

3

+1，通过解方程可以求得x的值；
（2）已知抛物线与x轴的两个交点的坐标，所以设“两点式”方程，把点A的坐标代入函数解析式，即利用待定系数法求得抛物线的解析式；
（3）存在t，使△POB的外心在x轴上，即△POB的外心在OB上．由圆周角定理推知∠OPB=90°，通过解Rt△OPB求得OP=

1

2

（

3

+1）=2t，由此求得t的值．

解答：解：（1）过点A作AC⊥OB于点C，设OC=x．
∵在Rt△AOC中，∠AOC=60°，
∴AC=

3

x．
又∵在Rt△ABC中，∠ABC=45°，
∴BC=

3

x．
∵OB=

3

+1，
∴OC+BC=OB，
∴x+

3

x=

3

+1，
∴x=1，AC=BC=

3

，
∴点A的坐标为：（1，

3

）；

（2）∵抛物线经过点A（1，

3

）、O（0，0）、B（

3

+1，0）．
∴设y=a（x-0）（x-

3

-1）（a≠0）．
则

3

=a（-

3

），
解得 a=-1．
故该抛物线的解析式为：y=-x²+（

3

+1）x；

（3）存在t，使△POB的外心在x轴上，即△POB的外心在OB上．理由如下：
∵△POB的外心在OB上，
∴∠OPB=90°（直径所对的圆周角是直角），
∴OP=OB•cos60°=

1

2

（

3

+1），
∴OP=2t，
∴t=

3 +1

4

，即当t=

3 +1

4

时，△POB的外心在x轴上．

点评：本题考查了二次函数综合题型．需要同学们掌握待定系数法求二次函数解析式、坐标与图形的性质，解直角三角形以及圆周角定理．在设抛物线解析式y=a（x-0）（x-

3

-1）时，一定要标明a≠0．