题目内容
 如图,在正方形ABCD中,点E、F分别是BC、CD的中点,DE交AF于点M,点N为DE的中点.
如图,在正方形ABCD中,点E、F分别是BC、CD的中点,DE交AF于点M,点N为DE的中点.(1)若AB=4,求△DNF的周长及sin∠DAF的值;
(2)求证:2AD•NF=DE•DM.
考点:正方形的性质,相似三角形的判定与性质,解直角三角形
专题:几何综合题
分析:(1)根据线段中点定义求出EC=DF=2,再利用勾股定理列式求出DE,然后三角形的中位线平行于第三边并且等于第三边的一半求出NF,再求出DN,再根据三角形的周长的定义列式计算即可得解;利用勾股定理列式求出AF,再根据锐角的正弦等于对边比斜边列式计算即可得解;
(2)利用“边角边”证明△ADF和△DCE全等,根据全等三角形对应边相等可得AF=DE,全等三角形对应角相等可得∠DAF=∠CDE,再求出AF⊥DE,然后根据三角形的中位线平行于第三边并且等于第三边的一半可得DF=EC=2NF,然后根据∠DAF和∠CDE的余弦列式整理即可得证.
(2)利用“边角边”证明△ADF和△DCE全等,根据全等三角形对应边相等可得AF=DE,全等三角形对应角相等可得∠DAF=∠CDE,再求出AF⊥DE,然后根据三角形的中位线平行于第三边并且等于第三边的一半可得DF=EC=2NF,然后根据∠DAF和∠CDE的余弦列式整理即可得证.
解答:(1)解:∵点E、F分别是BC、CD的中点,
∴EC=DF=
×4=2,
由勾股定理得,DE=
=2
,
∵点F是CD的中点,点N为DE的中点,
∴DN=
DE=
×2
=
,
NF=
EC=
×2=1,
∴△DNF的周长=1+
+2=3+
;
在Rt△ADF中,由勾股定理得,AF=
=
=2
,
所以,sin∠DAF=
=
=
;
(2)证明:在△ADF和△DCE中,
,
∴△ADF≌△DCE(SAS),
∴AF=DE,∠DAF=∠CDE,
∵∠DAF+∠AFD=90°,
∴∠CDE+∠AFD=90°,
∴AF⊥DE,
∵点N、F分别是DE、CD的中点,
∴NF是△CDE的中位线,
∴DF=EC=2NF,
∵cos∠DAF=
=
,
cos∠CDE=
=
,
∴
=
,
∴2AD•NF=DE•DM.
∴EC=DF=
| 1 |
| 2 |
由勾股定理得,DE=
| 22+42 |
| 5 |
∵点F是CD的中点,点N为DE的中点,
∴DN=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 5 |
NF=
| 1 |
| 2 |
| 1 |
| 2 |
∴△DNF的周长=1+
| 5 |
| 5 |
在Rt△ADF中,由勾股定理得,AF=
| AD2+DF2 |
| 42+22 |
| 5 |
所以,sin∠DAF=
| DF |
| AF |
| 2 | ||
2
|
| ||
| 5 |
(2)证明:在△ADF和△DCE中,
|

∴△ADF≌△DCE(SAS),
∴AF=DE,∠DAF=∠CDE,
∵∠DAF+∠AFD=90°,
∴∠CDE+∠AFD=90°,
∴AF⊥DE,
∵点N、F分别是DE、CD的中点,
∴NF是△CDE的中位线,
∴DF=EC=2NF,
∵cos∠DAF=
| AD |
| AF |
| AD |
| DE |
cos∠CDE=
| DM |
| DF |
| DM |
| 2NF |
∴
| AD |
| DE |
| DM |
| 2NF |
∴2AD•NF=DE•DM.
点评:本题考查了正方形的性质,三角形的中位线平行于第三边并且等于第三边的一半的,全等三角形的判定与性质,解直角三角形,锐角三角函数的定义,(2)求出三角形全等,再根据等角的余弦相等列出等式求解更简便.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
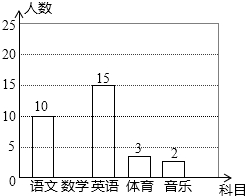 学习委员统计全班50位同学对语文、数学、英语、体育、音乐五个科目最喜欢情况,所得数据用表格与条形图描述如下:
学习委员统计全班50位同学对语文、数学、英语、体育、音乐五个科目最喜欢情况,所得数据用表格与条形图描述如下: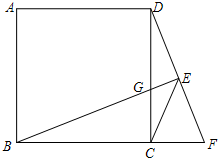 如图,在正方形ABCD 中,点F是BC延长线上一点,过点B作BE⊥DF于点E,交CD于点G,连接CE.
如图,在正方形ABCD 中,点F是BC延长线上一点,过点B作BE⊥DF于点E,交CD于点G,连接CE.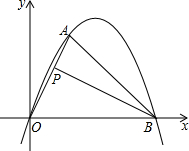 在平面直角坐标系中,B(
在平面直角坐标系中,B( 如图,AE是∠BAC的角平线,AE是中垂线PF交BC的延长线于点F,若∠CAF=50°,则∠B=
如图,AE是∠BAC的角平线,AE是中垂线PF交BC的延长线于点F,若∠CAF=50°,则∠B=