题目内容
14.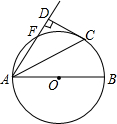 如图,AB是⊙O的直径,点F、C在⊙O上且$\widehat{BC}=\widehat{CF}$,连接AC、AF,过点C作CD⊥AF交AF的延长线于点D.
如图,AB是⊙O的直径,点F、C在⊙O上且$\widehat{BC}=\widehat{CF}$,连接AC、AF,过点C作CD⊥AF交AF的延长线于点D.(1)求证:CD是⊙O的切线;
(2)若$\widehat{AF}=\widehat{FC}$,CD=4,求⊙O的半径.
分析 (1)连结OC,由F,C,B三等分半圆,根据圆周角定理得∠FAC=∠BAC,而∠OAC=∠OCA,则∠FAC=∠OCA,可判断OC∥AF,由于CD⊥AF,所以OC⊥CD,然后根据切线的判定定理得到CD是⊙O的切线;
(2)连结BC,由AB为直径得∠ACB=90°,由F,C,B三等分半圆得∠BOC=60°,则∠BAC=30°,所以∠DAC=30°,在Rt△ADC中,利用含30度的直角三角形三边的关系得AC=2CD=8,在Rt△ACB中,根据勾股定理求得AB,进而求得⊙O的半径.
解答 (1)证明:连结OC,如图,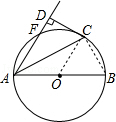
∵$\widehat{BC}=\widehat{CF}$,
∴∠FAC=∠BAC,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠FAC=∠OCA,
∴OC∥AF,
∵CD⊥AF,
∴OC⊥CD,
∴CD是⊙O的切线;
(2)解:连结BC,如图,
∵AB为直径,
∴∠ACB=90°,
∵$\widehat{BC}=\widehat{CF}$=$\widehat{AF}$,
∴∠BOC=$\frac{1}{3}$×180°=60°,
∴∠BAC=30°,
∴∠DAC=30°,
在Rt△ADC中,CD=4,
∴AC=2CD=8,
在Rt△ACB中,BC2+AC2=AB2,
即82+($\frac{1}{2}$AB)2=AB2,
∴AB=$\frac{16\sqrt{3}}{3}$,
∴⊙O的半径为$\frac{8\sqrt{3}}{3}$.
点评 本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了圆周角定理和含30度的直角三角形三边的关系.

练习册系列答案
相关题目
 如图,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PD=4,则PC的长为8.
如图,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PD=4,则PC的长为8. 如图,已知∠1=∠2,要得到△ABD≌△ACD,还需补充一个条件,则这个条件可以是AB=AC(答案不唯一).
如图,已知∠1=∠2,要得到△ABD≌△ACD,还需补充一个条件,则这个条件可以是AB=AC(答案不唯一).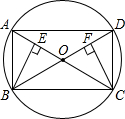 如图,在⊙O中,AC与BD是圆的直径,BE⊥AC,CF⊥BD,垂足分别为E、F
如图,在⊙O中,AC与BD是圆的直径,BE⊥AC,CF⊥BD,垂足分别为E、F ∶
∶ =2∶5,则
=2∶5,则 ∶
∶
 如图是一直径为2m的桶水管道的横截面图,其水面宽为1.6m,则这条管道中此时水的最大深度为0.4m.
如图是一直径为2m的桶水管道的横截面图,其水面宽为1.6m,则这条管道中此时水的最大深度为0.4m.