题目内容
2. 如图,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PD=4,则PC的长为8.
如图,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PD=4,则PC的长为8.
分析 由角平分线定理得到PE=PD,由平行线的性质和角平分线的定义得出∠COP=∠CPO,利用三角形外角的性质求出∠ECP=30°,在直角三角形ECP中,由30°角所对的直角边等于斜边的一半,即可得出结果.
解答 解:过P作PE⊥OB,交OB与点E,如图所示: ∵∠AOP=∠BOP,PD⊥OA,PE⊥OB,
∵∠AOP=∠BOP,PD⊥OA,PE⊥OB,
∴PE=PD=4,
∵PC∥OA,
∴∠CPO=∠POD,
又∠AOP=∠BOP=15°,
∴∠CPO=∠BOP=15°,
又∠ECP为△OCP的外角,
∴∠ECP=∠COP+∠CPO=30°,
在直角三角形CEP中,∠ECP=30°,
∴PC=2PE=8.
故答案为:8.
点评 此题考查了含30°角直角三角形的性质,角平分线定理,平行线的性质,以及三角形的外角性质;熟练掌握性质及定理是解本题的关键.同时注意辅助线的作法.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
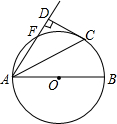 如图,AB是⊙O的直径,点F、C在⊙O上且$\widehat{BC}=\widehat{CF}$,连接AC、AF,过点C作CD⊥AF交AF的延长线于点D.
如图,AB是⊙O的直径,点F、C在⊙O上且$\widehat{BC}=\widehat{CF}$,连接AC、AF,过点C作CD⊥AF交AF的延长线于点D.