题目内容
5.阅读下列材料:“为什么$\sqrt{2}$不是有理数”.假设$\sqrt{2}$是有理数,那么存在两个互质的正整数m,n,使得$\sqrt{2}$=$\frac{n}{m}$,于是有2m2=n2.
∵2m2是偶数,∴n2也是偶数,∴n是偶数.
设n=2t(t是正整数),则n2=4t2,即4t2=2m2,
∴2t2=m2,
∴m也是偶数
∴m,n都是偶数,不互质,与假设矛盾.
∴假设错误,
∴$\sqrt{2}$不是有理数
有类似的方法,请证明$\sqrt{3}$不是有理数.
分析 根据题意利用反证法假设$\sqrt{3}$是有理数,进而利用假设得出矛盾,从而得出假设不成立原命题正确.
解答 解:假设$\sqrt{3}$是有理数,
则存在两个互质的正整数m,n,使得$\sqrt{3}$=$\frac{n}{m}$,
于是有3m2=n2,
∵3m2是3的倍数,
∴n2也是3的倍数,
∴n是3的倍数,
设n=3t(t是正整数),则n2=9t2,即9t2=3m2,
∴3t2=m2,
∴m也是3的倍数,
∴m,n都是3的倍数,不互质,与假设矛盾,
∴假设错误,
∴$\sqrt{3}$不是有理数.
点评 此题主要考查了实数的概念以及反证法的应用,正确掌握反证法的基本步骤是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,边长为$\sqrt{2}$的正方形ABCD的顶点A、B在一个半径为$\sqrt{2}$的圆上,顶点C、D在圆内,将正方形ABCD沿圆的内壁逆时针方向作无滑动的滚动.当点C第一次落在圆上时,点C运动的路径长为$({\frac{1}{3}+\frac{{\sqrt{2}}}{6}})π$.
如图,边长为$\sqrt{2}$的正方形ABCD的顶点A、B在一个半径为$\sqrt{2}$的圆上,顶点C、D在圆内,将正方形ABCD沿圆的内壁逆时针方向作无滑动的滚动.当点C第一次落在圆上时,点C运动的路径长为$({\frac{1}{3}+\frac{{\sqrt{2}}}{6}})π$. 如图,已知AD、BC相交于点O,AB∥CD∥EF,如果CE=2,EB=4,FD=1.5,那么AD=4.5.
如图,已知AD、BC相交于点O,AB∥CD∥EF,如果CE=2,EB=4,FD=1.5,那么AD=4.5.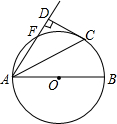 如图,AB是⊙O的直径,点F、C在⊙O上且$\widehat{BC}=\widehat{CF}$,连接AC、AF,过点C作CD⊥AF交AF的延长线于点D.
如图,AB是⊙O的直径,点F、C在⊙O上且$\widehat{BC}=\widehat{CF}$,连接AC、AF,过点C作CD⊥AF交AF的延长线于点D.