题目内容
4. 如图是一直径为2m的桶水管道的横截面图,其水面宽为1.6m,则这条管道中此时水的最大深度为0.4m.
如图是一直径为2m的桶水管道的横截面图,其水面宽为1.6m,则这条管道中此时水的最大深度为0.4m.
分析 作OC⊥AB于C,交$\widehat{AB}$于D,连接OA,由勾股定理求出OC,即可求解.
解答 解:如图所示:
作OC⊥AB于C,交$\widehat{AB}$于D,连接OA,
则OA=1m,AC=BC=$\frac{1}{2}$AB=0.8m.
在直角△OAC中,OC=$\sqrt{O{A}^{2}-A{C}^{2}}$=$\sqrt{{1}^{2}-0.{8}^{2}}$=0.6(m);
则水深CD=OD-OC=1-0.6=0.4(m);
故答案为:0.4.
点评 此题考查了垂径定理的运用、勾股定理;通过作辅助线运用垂径定理和勾股定理是解决问题的关键.

练习册系列答案
相关题目
9.飞机在飞行过程中,如果上升23米记作“+23米”,那么下降15米应记作( )
| A. | -8米 | B. | +8米 | C. | -15米 | D. | +15米 |
16.下列各式计算正确的是( )
| A. | (a5)2=a7 | B. | 2x-2=$\frac{1}{2{x}^{2}}$ | C. | 3a2•2a3=6a5 | D. | a6÷a6=0 |
13.如果把分式$\frac{3x}{x+y}$中的x和y的值都扩大5倍,那么分式的值( )
| A. | 扩大5倍 | B. | 缩小5倍 | C. | 不改变; | D. | 扩大25倍 |
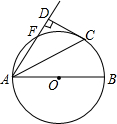 如图,AB是⊙O的直径,点F、C在⊙O上且$\widehat{BC}=\widehat{CF}$,连接AC、AF,过点C作CD⊥AF交AF的延长线于点D.
如图,AB是⊙O的直径,点F、C在⊙O上且$\widehat{BC}=\widehat{CF}$,连接AC、AF,过点C作CD⊥AF交AF的延长线于点D.
 如图是由五个相同的小正方体搭成的一个几何体,从上面看到的几何体的形状图是( )
如图是由五个相同的小正方体搭成的一个几何体,从上面看到的几何体的形状图是( )


