题目内容
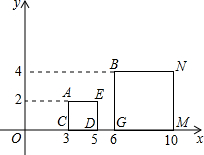 如图,在直角坐标系中,点A、B的坐标分别为(3,2)、(6,4),AC⊥x轴于点C,BG⊥x轴于点G,分别以AC、BG为边作正方形ACDE和正方形BGMN;
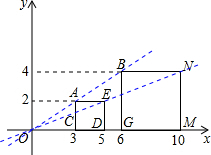
如图,在直角坐标系中,点A、B的坐标分别为(3,2)、(6,4),AC⊥x轴于点C,BG⊥x轴于点G,分别以AC、BG为边作正方形ACDE和正方形BGMN;(1)试分别写出直线AB和直线EN对应的函数表达式;
(2)求证:正方形ACDE和正方形BGMN是位似图形;
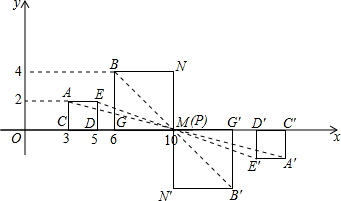
(3)已知点P的坐标是(10,0),试作一个正方形,它以点P为其中一个顶点,且与已有正方形成位似图形(在下图中作出即可).
考点:一次函数综合题,位似变换
专题:综合题
分析:(1)设直线AB解析式为y=kx+b(k≠0),将A与B坐标代入求出k与b的值,确定出直线AB解析式,根据正方形的性质得出E与N坐标,设直线EN解析式为y=px+q(p≠0),将E与N坐标代入求出p与q的值,即可确定出直线NE解析式;
(2)根据直线AB与直线NE都为正比例函数,图象过原点,直线DM,直线CG都与x轴重合,利用位似图形性质判断即可得证;
(3)以P为位似中心,做出正方形ACDE与正方形MNBG的位似图形即可.
(2)根据直线AB与直线NE都为正比例函数,图象过原点,直线DM,直线CG都与x轴重合,利用位似图形性质判断即可得证;
(3)以P为位似中心,做出正方形ACDE与正方形MNBG的位似图形即可.
解答:解:(1)设直线AB解析式为y=kx+b(k≠0),
将A(3,2),B(6,4)代入得:
,
解得:k=
,b=0,
∴直线AB解析式为y=
x;
根据题意得:E(5,2),N(10,4),
设直线EN解析式为y=px+q(p≠0),将E与N坐标代入得:
,
解得:p=
,q=0,
∴直线NE解析式为y=
x;
(2)∵直线AB解析式为y=
x与直线NE解析式为y=
x都过原点,直线DM与直线CG都与x轴重合,
∴正方形ACDE与正方形BGMN对应顶点连线交于一点,此点为原点,
则正方形ACDE和正方形BGMN是位似图形;
(3)如图所示,正方形MN′B′G′,正方形A′E′D′C′为所求的正方形.
将A(3,2),B(6,4)代入得:
|
解得:k=
| 2 |
| 3 |
∴直线AB解析式为y=
| 2 |
| 3 |
根据题意得:E(5,2),N(10,4),
设直线EN解析式为y=px+q(p≠0),将E与N坐标代入得:
|
解得:p=
| 2 |
| 5 |
∴直线NE解析式为y=
| 2 |
| 5 |
(2)∵直线AB解析式为y=
| 2 |
| 3 |
| 2 |
| 5 |
∴正方形ACDE与正方形BGMN对应顶点连线交于一点,此点为原点,
则正方形ACDE和正方形BGMN是位似图形;

(3)如图所示,正方形MN′B′G′,正方形A′E′D′C′为所求的正方形.

点评:此题属于一次函数综合题,涉及的知识有:待定系数法求一次函数解析式,位似图形的性质,以及正方形的性质,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
 如图,直线OC,BC的函数关系式分别是y1=x和y2=-x+6,两直线的交点为C.
如图,直线OC,BC的函数关系式分别是y1=x和y2=-x+6,两直线的交点为C. 如图,身高1.6米的小明从距路灯的底部(点O)20米的点A沿AO方向行走14米到点C处,小明在A处,头顶B在路灯投影下形成的影子在M处.
如图,身高1.6米的小明从距路灯的底部(点O)20米的点A沿AO方向行走14米到点C处,小明在A处,头顶B在路灯投影下形成的影子在M处.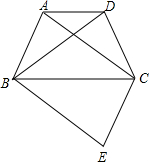 如图,四边形ABCD为等腰梯形,AD∥BC,连结AC、BD.在平面内将△DBC沿BC翻折得到△EBC.
如图,四边形ABCD为等腰梯形,AD∥BC,连结AC、BD.在平面内将△DBC沿BC翻折得到△EBC. 阅读理解
阅读理解