题目内容
在△ABC中，设∠A、∠B、∠C的边分别为a、b、c，若∠A：∠B：∠C=1：2：3，则a2：b2：c2= ．
考点：含30度角的直角三角形,勾股定理
专题：
分析：求出三角形ABC是直角三角形，求出c=2a，b=
a，代入求出即可．
| 3 |
解答：解：
∵∠A：∠B：∠C=1：2：3，∠A+∠B+∠C=180°，
∴∠A=30°，∠B=60°，∠C=90°，
∴c=2a，由勾股定理得：b=
=
a，
∴a2：b2：c2=a2：（
a）2：（2a）2=1：3：4，
故答案为：1：3：4．
∵∠A：∠B：∠C=1：2：3，∠A+∠B+∠C=180°，
∴∠A=30°，∠B=60°，∠C=90°，
∴c=2a，由勾股定理得：b=
| c2-a2 |
| 3 |
∴a2：b2：c2=a2：（
| 3 |
故答案为：1：3：4．
点评：本题考查了含30度角的直角三角形，勾股定理的应用，主要考查学生的计算能力．
练习册系列答案
举一反三同步巧讲精练系列答案
口算与应用题卡系列答案
名师点睛字词句段篇系列答案
相关题目
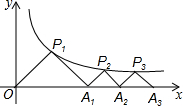如图所示，P1（x1，y1）、P2（x2，y2），…，Pn（xn，yn）在函数y=