题目内容
18.已知四边形ABCD中,AB∥CD,对角线AC与BD交于点O,下列条件中不能用作判定该四边形是平行四边形条件的是( )| A. | AB=CD | B. | AC=BD | C. | AD∥BC | D. | OA=OC |
分析 利用平行线的判定与性质结合平行四边形的判定得出即可.
解答 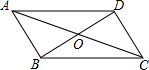 解:A、由AB∥CD、AB=CD可以判定该四边形是平行四边形,根据是“一组对边平行且相等的四边形是平行四边形”,故本选项错误;
解:A、由AB∥CD、AB=CD可以判定该四边形是平行四边形,根据是“一组对边平行且相等的四边形是平行四边形”,故本选项错误;
B、由AB∥CD、AC=BD不可以判定四边形ABCD是平行四边形,故本选项正确;
C、由AB∥CD、AD∥BC可以判定该四边形是平行四边形,根据是“两组对边分别平行的四边形是平行四边形”,故本选项错误;
D、由AB∥CD得到:∠DAO=∠BCO,在△DAO与△BCO中,$\left\{\begin{array}{l}{∠DAO=∠BCO}\\{OA=OC}\\{∠DOA=∠BOC}\end{array}\right.$,则△DAO≌△BCO(ASA),
所以OD=OB,
又OA=OC,
所以四边形ABCD是平行四边形,故本选项错误;
故选:B.
点评 本题考查了平行四边形的定义、平行四边形的判定定理;熟练掌握平行四边形的判定方法是解决问题的关键.

练习册系列答案
相关题目
6.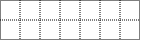 如图是小明家沙发坐垫的平面示意图,中间的双人沙发坐垫面积为2×3(单位面积),左右两边的是坐垫面积为2×2(单位面积)的单人沙发,小明和小虎在玩“藏密码”的游戏,已知小虎将密码藏在沙发坐垫下,则密码藏在单人沙发坐垫下的概率是( )
如图是小明家沙发坐垫的平面示意图,中间的双人沙发坐垫面积为2×3(单位面积),左右两边的是坐垫面积为2×2(单位面积)的单人沙发,小明和小虎在玩“藏密码”的游戏,已知小虎将密码藏在沙发坐垫下,则密码藏在单人沙发坐垫下的概率是( )
 如图是小明家沙发坐垫的平面示意图,中间的双人沙发坐垫面积为2×3(单位面积),左右两边的是坐垫面积为2×2(单位面积)的单人沙发,小明和小虎在玩“藏密码”的游戏,已知小虎将密码藏在沙发坐垫下,则密码藏在单人沙发坐垫下的概率是( )
如图是小明家沙发坐垫的平面示意图,中间的双人沙发坐垫面积为2×3(单位面积),左右两边的是坐垫面积为2×2(单位面积)的单人沙发,小明和小虎在玩“藏密码”的游戏,已知小虎将密码藏在沙发坐垫下,则密码藏在单人沙发坐垫下的概率是( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{7}$ | C. | $\frac{3}{7}$ | D. | $\frac{4}{7}$ |
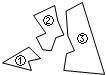 如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,现有以下几个方案:
如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,现有以下几个方案: 如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-1,0),与y轴的交点在(0,-2)和(0,-1)之间(不包括这两点),对称轴为直线x=1.下列结论:
如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-1,0),与y轴的交点在(0,-2)和(0,-1)之间(不包括这两点),对称轴为直线x=1.下列结论:
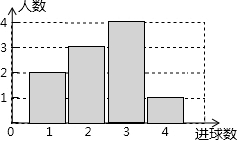 体育课上,老师为了解女学生定点投篮的情况,随机抽取10名女生进行每人4次定点投篮的测试,进球数的统计如图所示.
体育课上,老师为了解女学生定点投篮的情况,随机抽取10名女生进行每人4次定点投篮的测试,进球数的统计如图所示.