题目内容
3.已知直线y=kx+b(k≠0)过点(1,2)(1)填空:b=2-k(用含k代数式表示);
(2)将此直线向下平移2个单位,设平移后的直线交x于点A,交y于点B,x轴上另有点C(1+k,0),使得△ABC的面积为2,求k值;
(3)当1≤x≤3,函数值y总大于零,求k取值范围.
分析 (1)把点(1,2)代入y=kx+b(k≠0),得出k+b=2,即b=2-k;
(2)把b=2-k代入y=kx+b,得y=kx+2-k,根据上加下减的平移规律得出向下平移2个单位所得直线的解析式为y=kx-k,求出A(1,0),B(0,-k),根据△ABC的面积为2列出方程$\frac{1}{2}$k2=2,解方程即可;
(3)依题意,分两种情况讨论:ⅰ)当k>0时,y随x增大而增大,得出k+2-k=2>0;ⅱ)当k<0时,y随x增大而减小,得出3k+2-k=2k+2>0;分别解不等式即可.
解答 解:(1)∵直线y=kx+b(k≠0)过点(1,2),
∴k+b=2,
∴b=2-k.
故答案为2-k;
(2)由(1)可得y=kx+2-k,
向下平移2个单位所得直线的解析式为y=kx-k,
令x=0,得y=-k,令y=0,得x=1,
∴A(1,0),B(0,-k),
∵C(1+k,0),
∴AC=|1+k-1|=|k|,
∴S△ABC=$\frac{1}{2}$AC•|yB|=$\frac{1}{2}$|k|•|-k|=$\frac{1}{2}$k2,
∴$\frac{1}{2}$k2=2,解得k=±2;
(3)依题意,当自变量x在1≤x≤3变化时,函数值y的最小值大于0.
分两种情况:
ⅰ)当k>0时,y随x增大而增大,
∴当x=1时,y有最小值,最小值为k+2-k=2>0,
∴当 k>0时,函数值总大于0;
ⅱ)当k<0时,y随x增大而减小,
∴当x=3时,y有最小值,最小值为3k+2-k=2k+2,
由2k+2>0得k>-1,
∴-1<k<0.
综上,当k>0或-1<k<0时,函数值y总大于0.
点评 本题考查了一次函数图象与几何变换,一次函数图象上点的坐标特征,三角形的面积,一次函数的性质.难度适中.

 名校课堂系列答案
名校课堂系列答案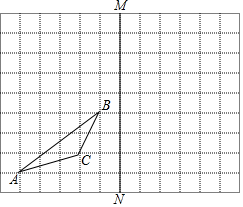 如图,已知三角形ABC和直线MN,且三角形ABC的顶点在网格的交点上.
如图,已知三角形ABC和直线MN,且三角形ABC的顶点在网格的交点上.(1)画出三角形ABC向上平移4小格后的三角形A1B1C1;
(2)画出三角形ABC关于直线MN成轴对称的三角形A2B2C2.
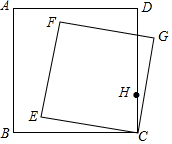 如图,正方形ABCD中,AB=4,点H在CD边上,且CH=1,点E绕点B旋转,同时,以CE为边在BC上方作正方形CEFG,在点E运动过程中,当线段FH取得最小值时,∠CBE的正切为( )
如图,正方形ABCD中,AB=4,点H在CD边上,且CH=1,点E绕点B旋转,同时,以CE为边在BC上方作正方形CEFG,在点E运动过程中,当线段FH取得最小值时,∠CBE的正切为( )| A. | $\frac{1}{5}$ | B. | $\frac{\sqrt{2}}{5}$ | C. | $\frac{\sqrt{2}}{7}$ | D. | $\frac{1}{7}$ |
| A. | AB=CD | B. | AC=BD | C. | AD∥BC | D. | OA=OC |
| A. | 众数是80 | B. | 中位数是75 | C. | 平均数是80 | D. | 极差是15 |




 已知:如图,△ABC中,AB=4,AC=6,AD平分∠BAC,且BD⊥AD于D,交AC于F,E是BC的中点,连接DE.求:DE的长度.
已知:如图,△ABC中,AB=4,AC=6,AD平分∠BAC,且BD⊥AD于D,交AC于F,E是BC的中点,连接DE.求:DE的长度. 如图,已知AB∥CD,∠1=∠2,那么AE与DF平行吗?试说明理由.
如图,已知AB∥CD,∠1=∠2,那么AE与DF平行吗?试说明理由.