题目内容
19.已知一元二次方程x2+(2k+1)x+k+$\frac{3}{4}$=0有两个不相等的实数根,求k的取值范围.分析 由方程由两个不等实数根可得b2-4ac>0,代入数据即可得出关于k的一元二次不等式,解方程即可得出结论.
解答 解:由已知得:△=b2-4ac=(2k+1)2-4(k+$\frac{3}{4}$)>0,
即2k2-1>0,
解得:k<-$\frac{\sqrt{2}}{2}$或k>$\frac{\sqrt{2}}{2}$.
答:k的取值范围为:k<-$\frac{\sqrt{2}}{2}$或k>$\frac{\sqrt{2}}{2}$.
点评 本题考查了根的判别式以及解一元二次不等式,解题的关键是找出关于k的一元二次不等式.本题属于基础题,难度不大,解决该题型题目时,根据根的个数结合根的判别式得出不等式(或不等式组)是关键.

练习册系列答案
相关题目
7.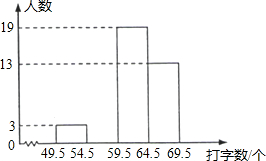 初三(1)班共有40名同学,在一次30秒打字速度测试中他们的成绩统计如表:
初三(1)班共有40名同学,在一次30秒打字速度测试中他们的成绩统计如表:
(1)将这些数据按组距5(个字)分组,绘制成如图的频数分布直方图(不完整),请将表中空缺的数据填写完整,并补全频数分布直方图;
(2)若将频数分布直方图转化为扇形统计图,则打字数在54.5-59.5这一段所在扇形的圆心角的度数是多少?
 初三(1)班共有40名同学,在一次30秒打字速度测试中他们的成绩统计如表:
初三(1)班共有40名同学,在一次30秒打字速度测试中他们的成绩统计如表:| 打字数/个 | 50 | 51 | 59 | 62 | 64 | 66 | 69 |
| 人数 | 1 | 2 | 8 | 11 | 5 |
(2)若将频数分布直方图转化为扇形统计图,则打字数在54.5-59.5这一段所在扇形的圆心角的度数是多少?
 如图,四边形ABCD为菱形,E为对角线BD延长线上一点,且BD=4,DE=1,∠BAE=45°,则AB=2$\sqrt{10}$.
如图,四边形ABCD为菱形,E为对角线BD延长线上一点,且BD=4,DE=1,∠BAE=45°,则AB=2$\sqrt{10}$. 如图,已知△ABC,求作BC边上的高.(尺规作图,保留痕迹)
如图,已知△ABC,求作BC边上的高.(尺规作图,保留痕迹) 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$(x>0)的图象交于点P(n,2),与x轴交于点A,与y轴交于点C,PB⊥x轴于点B,且AC=BC,S△PBC=4.
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$(x>0)的图象交于点P(n,2),与x轴交于点A,与y轴交于点C,PB⊥x轴于点B,且AC=BC,S△PBC=4. 如图,若点A的坐标为$(1,\sqrt{3})$,则sin∠1=$\frac{{\sqrt{3}}}{2}$.
如图,若点A的坐标为$(1,\sqrt{3})$,则sin∠1=$\frac{{\sqrt{3}}}{2}$. 矩形DEFG的四个顶点分别在Rt△ABC的边上,∠A=90°,在Rt△DGC和Rt△BFE内又作如图所示的正方形JGHI和正方形KFML,求证:ID=EL.
矩形DEFG的四个顶点分别在Rt△ABC的边上,∠A=90°,在Rt△DGC和Rt△BFE内又作如图所示的正方形JGHI和正方形KFML,求证:ID=EL.