Question

1．如图，矩形ABCD的一条对称轴恰好是y轴，AB边在x轴上，把矩形ABCD沿着对角线BD折叠，点A恰好落在y轴上的E（0，2$\sqrt{3}$）点处，则阴影部分的面积是$\frac{8\sqrt{3}}{9}$．

Answer 1

分析 设BD与y轴的交点为F，BF与CD交于点M，∠ABD=x，先求出x，推出△DEF是等边三角形，推出EO=3OF，求出OF，再求出AD、AE、EM即可解决问题．

解答 解：设BD与y轴的交点为F，BF与CD交于点M，∠ABD=x，
∵AO=BO．OF∥AD，
∴DF=FB，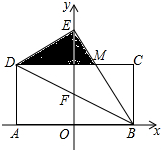
∵∠DEB=90°，
∴EF=DF=BF，
∴∠ABD=∠DBE=∠BEF=x，
∴∠EFD=∠BFO=∠FBE+∠FEB=2x，
∴2x+x=90°，
∴x=30°，∴∠CDB=∠ABD=30°，∠BDE=60°，∠EDC=30°，
∴△EDF是等边三角形，
∵AD=DE=EF=2FO，
∴3FO=EO=2$\sqrt{3}$，
∴OF=$\frac{2\sqrt{3}}{3}$，
∴AD=DE=$\frac{4\sqrt{3}}{3}$，
在RT△DEM中，∵∠DEM=90°，∠EDM=30°，DE=$\frac{4\sqrt{3}}{3}$，
∴EM=$\frac{4}{3}$，
∴S_阴=$\frac{1}{2}$•DE•EM=$\frac{8\sqrt{3}}{9}$．
故答案为$\frac{8\sqrt{3}}{9}$．

点评 本题考查矩形的性质、翻折变换、直角三角形斜边中线定理、等边三角形的判定和性质直角三角形30度角的性质等知识，解题的关键是灵活运用这些知识解决问题，属于中考常考题型．