题目内容
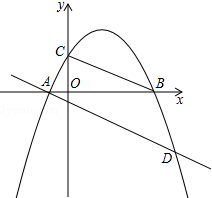 如图,已知抛物线y=ax2+bx+c(a≠0)经过A(-1,0),B(4,0),C(0,2)三点.
如图,已知抛物线y=ax2+bx+c(a≠0)经过A(-1,0),B(4,0),C(0,2)三点.(1)求这条抛物线的解析式;
(2)E为抛物线上一动点,是否存在点E使以A、B、E为顶点的三角形与△COB相似?若存在,试求出点E的坐标;若不存在,请说明理由.
考点:二次函数综合题
专题:
分析:(1)本题需先根据已知条件,过C点,设出该抛物线的解析式为y=ax2+bx+2,再根据过A,B两点,即可得出结果;
(2)由图象可知,以A、B为直角顶点的△ABE不存在,所以△ABE只可能是以点E为直角顶点的三角形.由相似关系求出点E的坐标.
(2)由图象可知,以A、B为直角顶点的△ABE不存在,所以△ABE只可能是以点E为直角顶点的三角形.由相似关系求出点E的坐标.
解答:解:(1)∵该抛物线过点C(0,2),
∴可设该抛物线的解析式为y=ax2+bx+2.
将A(-1,0),B(4,0)代入,
得
,解得
,
∴抛物线的解析式为:y=-
x2+
x+2.
(2)存在.
由图象可知,以A、B为直角顶点的△ABE不存在,所以△ABE只可能是以点E为直角顶点的三角形.
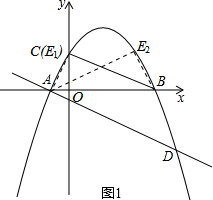
在Rt△BOC中,OC=2,OB=4,
∴BC=
=2
.
在Rt△BOC中,设BC边上的高为h,则
×2
h=
×2×4,
∴h=
.
∵△BEA∽△COB,设E点坐标为(x,y),
∴
=
,
∴y=±2
将y=2代入抛物线y=-
x2+
x+2,
得x1=0,x2=3.
当y=-2时,不合题意舍去.
∴E点坐标为(0,2),(3,2).
∴可设该抛物线的解析式为y=ax2+bx+2.
将A(-1,0),B(4,0)代入,
得
|
|
∴抛物线的解析式为:y=-
| 1 |
| 2 |
| 3 |
| 2 |
(2)存在.
由图象可知,以A、B为直角顶点的△ABE不存在,所以△ABE只可能是以点E为直角顶点的三角形.

在Rt△BOC中,OC=2,OB=4,
∴BC=
| 22+42 |
| 5 |
在Rt△BOC中,设BC边上的高为h,则
| 1 |
| 2 |
| 5 |
| 1 |
| 2 |
∴h=
| 4 |
| 5 |
| 5 |
∵△BEA∽△COB,设E点坐标为(x,y),
∴
| AB |
| BC |
| |y| | ||||
|
∴y=±2
将y=2代入抛物线y=-
| 1 |
| 2 |
| 3 |
| 2 |
得x1=0,x2=3.
当y=-2时,不合题意舍去.
∴E点坐标为(0,2),(3,2).
点评:本题考查了二次函数的综合题,涉及相似三角形的性质的运用,勾股定理的运用,解题的关键是正确求出函数的解析式.

练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
在平面直角坐标系xOy中,以点(3,4)为圆心,4为半径的圆与y轴所在直线的位置关系是( )
| A、相离 | B、相切 |
| C、相交 | D、无法确定 |
武汉市希望中学开展以“我最喜欢的职业”为主题的调查活动,通过对学生的随机抽样调查得到一组数据,如图是根据这组数据绘制的不完整的统计图,则下列说法中,不正确的是( )
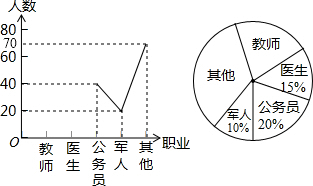

| A、被调查的学生有200人 |
| B、扇形图中公务员部分所对应的圆心角为72° |
| C、被调查的学生中喜欢其他职业的占40% |
| D、被调查的学生中喜欢教师职业的有40人 |
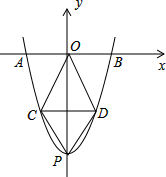 已知抛物线y=x2-8与x轴相交于两点A,B,与y轴相交于点P,
已知抛物线y=x2-8与x轴相交于两点A,B,与y轴相交于点P,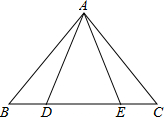 如图D,E是边BC上的两点,AD=AE,∠ADE=∠AED,利用“AAS”方法,请你再添加一个条件:
如图D,E是边BC上的两点,AD=AE,∠ADE=∠AED,利用“AAS”方法,请你再添加一个条件: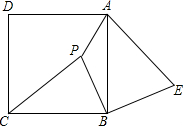 已知:如图,P是正方形ABCD内一点,在正方形ABCD外有一点E,满足∠ABE=∠CBP,BE=BP.
已知:如图,P是正方形ABCD内一点,在正方形ABCD外有一点E,满足∠ABE=∠CBP,BE=BP.