题目内容
在东营市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,已知每台电脑、每台电子白板各0.5万元和1.5万元.根据学校实际情况,须进购电脑和电子白板共30台,总费用不超过30万,但不低于28万元,请你通过计算求出有几种购进方案,哪种方案费用最低.
考点:一元一次不等式组的应用
专题:
分析:设购买电脑x台,则电子白板(30-x)台,购买的总费用为W元,由总费用=购买电脑的费用+购买电子白板的费用就可以表示出W与x的关系式,由一次函数的性质结合由总价不超过30万,不低于28万元建立一元一次不等式组的解就可以得出结论.
解答:解:设购买电脑x台,则电子白板(30-x)台,由题意,得
,
解得:15≤x≤17.
∵x为正整数,
∴x=15,16,17.
∴共有3种购进方案.
方案1,购买电脑15台,电子白板15台;
方案2,购买电脑16台,电子白板14台;
方案3,购买电脑17台,电子白板13台;
设购买的总费用为W元,由题意,得
W=0.5x+1.5(30-x),
W=-x+45,
∴k=-1<0,
∴W随x的增大二而减小,
∴当x=17时,w最小=28.
答:共有3中购进方案,方案3,购买电脑17台,电子白板13台的费用最少为28万元.
|
解得:15≤x≤17.
∵x为正整数,
∴x=15,16,17.
∴共有3种购进方案.
方案1,购买电脑15台,电子白板15台;
方案2,购买电脑16台,电子白板14台;
方案3,购买电脑17台,电子白板13台;
设购买的总费用为W元,由题意,得
W=0.5x+1.5(30-x),
W=-x+45,
∴k=-1<0,
∴W随x的增大二而减小,
∴当x=17时,w最小=28.
答:共有3中购进方案,方案3,购买电脑17台,电子白板13台的费用最少为28万元.
点评:本题考查了列一元一次不等式组解实际问题的运用,一元一次不等式组的解法的运用,方案设计的运用,一次函数的性质的运用,解答时建立不等式组求出其解是关键.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
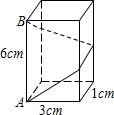 如图,长方体的底面边长为1cm和3cm,高为6cm.如果用一根细线从点A开始经过4个侧面缠绕一圈到达B,那么所用细线最短需要( )
如图,长方体的底面边长为1cm和3cm,高为6cm.如果用一根细线从点A开始经过4个侧面缠绕一圈到达B,那么所用细线最短需要( )| A、12cm | B、11cm |
| C、10cm | D、9cm |
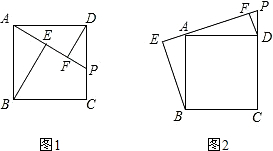
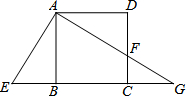 如图,四边形ABCD是正方形,点E在CB的延长线上,连结AE,将△ABE绕点A逆时针旋转90°,得到△ADF,点E落在DC上的点F处,AF的延长线交BC延长线于点G.若AB=3,AE=
如图,四边形ABCD是正方形,点E在CB的延长线上,连结AE,将△ABE绕点A逆时针旋转90°,得到△ADF,点E落在DC上的点F处,AF的延长线交BC延长线于点G.若AB=3,AE=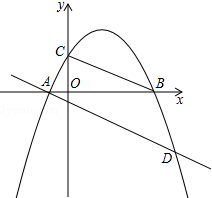 如图,已知抛物线y=ax2+bx+c(a≠0)经过A(-1,0),B(4,0),C(0,2)三点.
如图,已知抛物线y=ax2+bx+c(a≠0)经过A(-1,0),B(4,0),C(0,2)三点.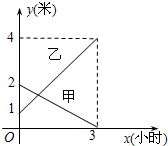 自来水公司有甲、乙两个蓄水池,现将甲池的中水匀速注入乙池,甲、乙两个蓄水池中水的深度y(米)与注水时间x(时)之间的函数图象如下所示,结合图象回答下列问题.
自来水公司有甲、乙两个蓄水池,现将甲池的中水匀速注入乙池,甲、乙两个蓄水池中水的深度y(米)与注水时间x(时)之间的函数图象如下所示,结合图象回答下列问题.