题目内容
15.3.12植树节,某校决定组织甲乙两队参加义务植树活动,并购买队服.表是服装厂给出的服装的价格表:| 购买服装的套数 | 1~39套 | 40~79套 | 80套及以上 |
| 每套服装的价格 | 80元 | 70元 | 60元 |
(1)如果甲、乙两队联合起来购买服装,那么比各自购买服装最多可以节省800元.
(2)甲、乙两队各有多少名学生?
(3)到了现场,因工作分配需要,临时决定从甲队抽调a人,从乙队抽调b人,组成丙队(要求从每队抽调的人数不少于10人).现已知重新组队后,甲队平均每人需植树1棵;乙队平均每人需植树4棵;丙队平均每人需植树6棵,甲乙丙三队共需植树265棵,请直接写出所有的抽调方案.
分析 (1)若甲、乙两个队合起来购买服装,则每套是70元,计算出总价,即可求得比各自购买服装共可以节省多少钱;
(2)设甲、乙队各有x名、y名学生准备参加演出.根据题意,显然各自购买时,甲乐团每套服装是70元,乙乐团每套服装是80元.根据等量关系:①共75人;②分别单独购买服装,一共应付5600元,列方程组即可求解;
(3)利用甲队平均每人需植树1棵;乙队平均每人需植树4棵;丙队平均每人需植树6棵,甲乙丙三队共需植树265棵列出方程探讨答案即可.
解答 解:(1)买80套所花费为:80×60=4800(元),
最多可以节省:5600-4800=800(元).
故答案是:800.
(2)解:设甲队有x人;乙队有y人.
根据题意,得
$\left\{\begin{array}{l}{x+y=75}\\{70x+80y=5600}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=40}\\{y=35}\end{array}\right.$,
答:甲队有40人;乙队有35人.
(3)由题意,得6(a+b)+(40-a)+4(35-b)=265,
整理,得b=$\frac{85-5a}{2}$
因为要求从每队抽调的人数不少于10人且人数为正整数
得$\left\{\begin{array}{l}{a=13}\\{b=10}\end{array}\right.$或$\left\{\begin{array}{l}{a=11}\\{b=15}\end{array}\right.$.
所以共有两种方案:从甲队抽调13人,从乙乐团抽调10人;或者从甲队抽调11人,从乙队抽调15人.
点评 此题考查二元一次方程组与二元一次方程的实际运用,分析题意,找到关键描述语,找到合适的等量关系是解决问题的关键.

 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案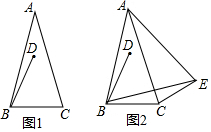 在△ABC中,AB=AC,∠BAC=α(0°<α<60°),BD=BC,∠DBC=60°.
在△ABC中,AB=AC,∠BAC=α(0°<α<60°),BD=BC,∠DBC=60°.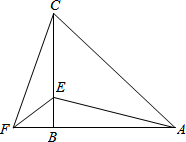 在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.
在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF. 如图,AB是⊙O的直径,AC、BC是⊙O的弦,∠ACB的平分线交⊙O于D,连接AD、BD,已知AB=6,BC=2.
如图,AB是⊙O的直径,AC、BC是⊙O的弦,∠ACB的平分线交⊙O于D,连接AD、BD,已知AB=6,BC=2.