题目内容
4．
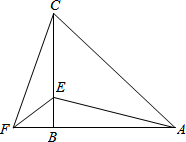在△ABC中，AB=CB，∠ABC=90°，F为AB延长线上一点，点E在BC上，且AE=CF．（1）求证：△ABE≌△CBF；
（2）若∠CAE=25°，求∠BFC度数．
分析 （1）根据HL证明Rt△ABE≌Rt△CBF；
（2）因为△ABC是等腰直角三角形，所以∠BAC=45°，得∠BAE=20°，由（1）中的全等得：∠BCF=∠BAE=20°，从而得出结论．
解答 （1）证明：∵∠ABC=90°，
∴∠ABC=∠CBF=90°，
在Rt△ABE和Rt△CBF中，
∵$\left\{\begin{array}{l}{AE=CF}\\{AB=CB}\end{array}\right.$，
∴Rt△ABE≌Rt△CBF（HL）；
（2）解：∵AB=CB，∠ABC=90°，
∴∠CAB=∠ACB=45°，
∵∠CAE=25°，
∴∠BAE=45°-25°=20°，
∵Rt△ABE≌Rt△CBF，
∴∠BCF=∠BAE=20°，
∴∠BFC=90°-20°=70°．
点评 本题考查了等腰直角三角形的性质和直角三角形全等的性质和判定，知道等腰直角三角形的两个锐角是45°，除了熟知三角形一般的全等判定方法外，还要掌握直角三角形的全等判定HL：即有一直角边和斜边对应相等的两直角三角形全等．
练习册系列答案
相关题目
如图所示，在平面直角坐标系中，菱形MNPO的顶点P的坐标是（3，4），则顶点N的坐标分别是（8，4）．
15．3.12植树节，某校决定组织甲乙两队参加义务植树活动，并购买队服．表是服装厂给出的服装的价格表：
经调查：两个队共75人（甲队人数不少于40人），如果分别各自购买队服，两队共需花费5600元，请回答以下问题：
（1）如果甲、乙两队联合起来购买服装，那么比各自购买服装最多可以节省800元．
（2）甲、乙两队各有多少名学生？
（3）到了现场，因工作分配需要，临时决定从甲队抽调a人，从乙队抽调b人，组成丙队（要求从每队抽调的人数不少于10人）．现已知重新组队后，甲队平均每人需植树1棵；乙队平均每人需植树4棵；丙队平均每人需植树6棵，甲乙丙三队共需植树265棵，请直接写出所有的抽调方案．
| 购买服装的套数 | 1～39套 | 40～79套 | 80套及以上 |
| 每套服装的价格 | 80元 | 70元 | 60元 |
（1）如果甲、乙两队联合起来购买服装，那么比各自购买服装最多可以节省800元．
（2）甲、乙两队各有多少名学生？
（3）到了现场，因工作分配需要，临时决定从甲队抽调a人，从乙队抽调b人，组成丙队（要求从每队抽调的人数不少于10人）．现已知重新组队后，甲队平均每人需植树1棵；乙队平均每人需植树4棵；丙队平均每人需植树6棵，甲乙丙三队共需植树265棵，请直接写出所有的抽调方案．
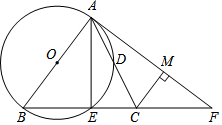如图，在△ABC中，AB=BC，以AB为直径的⊙O分别交AC，BC于点D，E，过点A作⊙O的切线交BC的延长线于点F，连接AE．