题目内容
20.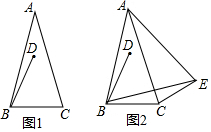 在△ABC中,AB=AC,∠BAC=α(0°<α<60°),BD=BC,∠DBC=60°.
在△ABC中,AB=AC,∠BAC=α(0°<α<60°),BD=BC,∠DBC=60°.(1)如图1,直接写出∠ABD的度数(用含α的式子表示);
(2)加图2,∠BCE=150°,∠ABE=60°,判断△ABE的形状并说明理由;
(3)在(2)的条件下,连接DE,若∠DEC=45°,求α的值.
分析 (1)根据等边对等角得出∠ABC=∠ACB,再根据三角形的内角和定理得出∠ABC=90°-$\frac{1}{2}$,最后根据∠DBC=60°,即可得出答案;
(2)连接AD,先证出△ABD≌△ACD,得出∠ADB=∠ADC,再根据∠BDC=60°,求出∠ADB=150°,得出∠ADB=∠BCE,再证出∠ABD=∠EBC,在△ABD和△EBC中,根据ASA得出△ABD≌△EBC,从而得出AB=BE,即可证出△ABE是等边三角形;
(3)根据已知条件先求出∠DCE=90°,再根据∠DEC=45°,得出△DEC为等腰直角三角形,再根据∠BAD=∠ABD=15°,∠BAC=30°,从而求出α的值.
解答 解:(1)∵AB=AC,
∴∠ABC=∠ACB,
∵∠BAC=α,
∴∠ABC=$\frac{180°-α}{2}$=90°-$\frac{1}{2}α$,
∵△DBC为等边三角形,
∴∠DBC=60°,
∴∠ABD=∠ABC-∠DBC=90°-$\frac{1}{2}α$-60°=30°-$\frac{1}{2}$α;
(2)△ABE是等边三角形;
如图2,
理由如下:连接AD,DE,DC
∵△DBC为等边三角形,
∴BD=CD,
∵AB=AC,
在△ABD和△ACD中,
$\left\{\begin{array}{l}{AB=AC}\\{AD=AD}\\{DB=DC}\end{array}\right.$,
∴△ABD≌△ACD(SSS),
∴∠ADB=∠ADC,
∵∠BDC=60°,
∴∠ADB=$\frac{360°-60°}{2}$=150°,
∴∠ADB=∠BCE,
∵∠ABE=60°,∠DBC=60°,
∴∠ABD=∠EBC,
在△ABD和△EBC中,
$\left\{\begin{array}{l}{∠ABD=∠EBC}\\{BD=BC}\\{∠ADB=∠BCE}\end{array}\right.$,
∴△ABD≌△EBC(ASA),
∴AB=BE,
∴△ABE是等边三角形;
(3)∵∠BCD=60°,∠BCE=150°,
∴∠DCE=150°-60°=90°,
∵∠DEC=45°,
∴△DEC为等腰直角三角形,
∴DC=CE=BD,
∵△DBC为等边三角形,
∴BC=CE,
∴∠CBE=∠BEC
∵∠BCE=150°,
∴∠BEC=$\frac{1}{2}$(180°-150°)=15°,
∵△ABD≌△EBC
∴∠BAD=∠ABD=∠BEC=15°,
∴∠ABC=∠ABD+∠DBC=75°
∵AB=AC,
∴∠BAC=30°,
∴α=30°.
点评 此题是三角形综合题,主要考查了全等三角形的判定与性质,用到的知识点是等边三角形的性质、全等三角形的判定与性质、三角形的内角和定理,关键是找出全等三角形.

 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案| 购买服装的套数 | 1~39套 | 40~79套 | 80套及以上 |
| 每套服装的价格 | 80元 | 70元 | 60元 |
(1)如果甲、乙两队联合起来购买服装,那么比各自购买服装最多可以节省800元.
(2)甲、乙两队各有多少名学生?
(3)到了现场,因工作分配需要,临时决定从甲队抽调a人,从乙队抽调b人,组成丙队(要求从每队抽调的人数不少于10人).现已知重新组队后,甲队平均每人需植树1棵;乙队平均每人需植树4棵;丙队平均每人需植树6棵,甲乙丙三队共需植树265棵,请直接写出所有的抽调方案.
 已知抛物线y=x2-2x-3与x轴相交于A、B两点,其顶点为M,将此抛物线在x轴下方的部分沿x轴翻折,其余部分保持不变,得到一个新的图象.如图,当直线y=-x+n与此图象有且只有两个公共点时,则n的取值范围为n>$\frac{21}{4}$或-1<n<3.
已知抛物线y=x2-2x-3与x轴相交于A、B两点,其顶点为M,将此抛物线在x轴下方的部分沿x轴翻折,其余部分保持不变,得到一个新的图象.如图,当直线y=-x+n与此图象有且只有两个公共点时,则n的取值范围为n>$\frac{21}{4}$或-1<n<3.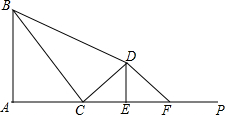 如图,∠A=90°,AB=6,点C是射线AP上的动点,连结BC,过点C作CD⊥BC,垂足为C,且BC=2CD,过点D作DE⊥AP于点E,点F是点C关于直线DE的对称点,连接BD、DF,设AC=m.
如图,∠A=90°,AB=6,点C是射线AP上的动点,连结BC,过点C作CD⊥BC,垂足为C,且BC=2CD,过点D作DE⊥AP于点E,点F是点C关于直线DE的对称点,连接BD、DF,设AC=m. 如图,△ABC中,BC=4,∠BAC=60°,且AB≠AC,若∠A的内外角平分线分别交BC的中垂线于D、E,试求DE的长度.
如图,△ABC中,BC=4,∠BAC=60°,且AB≠AC,若∠A的内外角平分线分别交BC的中垂线于D、E,试求DE的长度.