题目内容
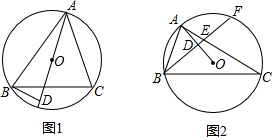
12.已知△ABC内接于⊙O,BD⊥AO于点D.(1)如图1,求证:∠ABD=∠ACB;
(2)如图2,延长BD,依次交AC,⊙O于点E,F,若∠ABC=2∠ACB,求证:BF=AC;
(3)如图3,在(2)的条件下,连接FO并延长,交AC边于点G,交BC边于点H,若FH=6,AB=5,求线段OH的长.
分析 (1)如图1中,延长AD交⊙O于H,连接BH.首先证明∠ABD=∠H,由∠H=∠ACB即可证明.
(2)由(1)可知,∠ABD=∠ACB,由∠ABC=2∠ACB,推出∠FBC=∠C,推出$\widehat{FC}$=$\widehat{AB}$,推出$\widehat{BF}$=$\widehat{AC}$,推出BF=AC.
(3)如图3中,连接AF、CF、AH.首先证明四边形AFCH是平行四边形,推出FG=GH=3,在Rt△AGF中,AG=$\sqrt{A{F}^{2}-F{G}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,设OA=OF=r,
在Rt△AOG中,由OA2=AG2+OG2,可得r2=42+(r-3)2,求出r即可解决问题.
解答 (1)证明:如图1中,延长AD交⊙O于H,连接BH.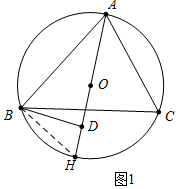
∵AB是直径,
∴∠ABH=90°,
∴∠ABD+∠HBD=90°,
∵BD⊥AH,
∴∠BDH=90°,
∴∠H+∠HBD=90°,
∴∠H=∠ABD,
∵∠H=∠ACB,
∴∠ABD=∠ACB.
(2)证明:如图2中,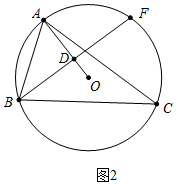
由(1)可知,∠ABD=∠ACB,
∵∠ABC=2∠ACB,
∴∠FBC=∠C,
∴$\widehat{FC}$=$\widehat{AB}$,
∴$\widehat{BF}$=$\widehat{AC}$,
∴BF=AC.
(3)解:如图3中,连接AF、CF、AH.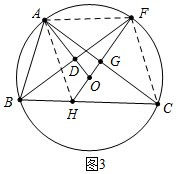
由(2)可知∠ABF=∠ACB=∠FBC=∠ACF,
∴$\widehat{AF}$=$\widehat{FC}$=$\widehat{AB}$,
∴AF=FC=AB=5,OF⊥AC,∠FAC=∠ACB,
∴AG=GC,AF∥CH,
在△AFG和△CHG中,
$\left\{\begin{array}{l}{∠FAG=∠HCG}\\{AG=GC}\\{∠AGF=∠CGH}\end{array}\right.$,
∴△AFG≌△CHG,
∴AF=CH,
∴四边形AFCH是平行四边形,
∴FG=GH=3,
在Rt△AGF中,AG=$\sqrt{A{F}^{2}-F{G}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,设OA=OF=r,
在Rt△AOG中,∵OA2=AG2+OG2,
∴r2=42+(r-3)2,
解得r=$\frac{25}{6}$,
∴OG=$\frac{7}{6}$,
∴OH=GH-OG=3-$\frac{7}{6}$=$\frac{11}{6}$.
点评 本题考查圆综合题、圆周角定理、全等三角形的判定和性质、勾股定理、平行四边形的判定和性质等知识,解题的关键是灵活运用所学知识,学会添加常用辅助线,构造特殊四边形解决问题,属于中考压轴题.

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案 如图:已知直线y=x+1与坐标轴相交于点A,B;现把抛物线y=-x2的图象平移,使它的图象经过点A,B两点,则平移的方法是( )
如图:已知直线y=x+1与坐标轴相交于点A,B;现把抛物线y=-x2的图象平移,使它的图象经过点A,B两点,则平移的方法是( )| A. | 向左平移一个单位 | B. | 向右平移一个单位 | ||
| C. | 向上平移一个单位 | D. | 向下平移一个单位 |
| A. | 人长生不老 | |
| B. | 2016年奥运会中国队获100枚金牌 | |
| C. | 掷两枚质地均匀的正方体骰子朝上一面的点数之积为21 | |
| D. | 一个星期为七天 |
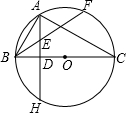 如图,已知BC是⊙O的直径,AH⊥BC,垂足为D,点A为$\widehat{BF}$的中点,BF交AD于点E,且BE•EF=32,AD=6
如图,已知BC是⊙O的直径,AH⊥BC,垂足为D,点A为$\widehat{BF}$的中点,BF交AD于点E,且BE•EF=32,AD=6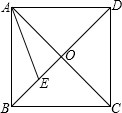 如图,正方形ABCD的边长为2,对角线AC、BD相交于点O,AE平分∠BAC交BD于E,则DE的长为2.
如图,正方形ABCD的边长为2,对角线AC、BD相交于点O,AE平分∠BAC交BD于E,则DE的长为2.