题目内容
4.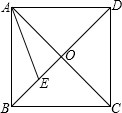 如图,正方形ABCD的边长为2,对角线AC、BD相交于点O,AE平分∠BAC交BD于E,则DE的长为2.
如图,正方形ABCD的边长为2,对角线AC、BD相交于点O,AE平分∠BAC交BD于E,则DE的长为2.
分析 如图作EH⊥AB于H.由EA平分∠BAO,EH⊥AB,EO⊥AC,推出EH=EO,设EH=EO=a,则BE=$\sqrt{2}$a,可得a+$\sqrt{2}$a=$\sqrt{2}$,解得a=2-$\sqrt{2}$,由此解决问题.(也可以证明∠DAE=∠DEA=67.5°,推出DA=DE=2.)
解答 解:如图作EH⊥AB于H.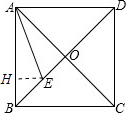
∵四边形ABCD是正方形,
∴AB=BC=CD=AD=2,BD=AC=2$\sqrt{2}$,OD=OB=$\sqrt{2}$,
∵EA平分∠BAO,EH⊥AB,EO⊥AC,
∴EH=EO,设EH=EO=a,则BE=$\sqrt{2}$a,
∴a+$\sqrt{2}$a=$\sqrt{2}$,解得a=2-$\sqrt{2}$,
∴DE=OD+OE=$\sqrt{2}$+2-$\sqrt{2}$=2.
(也可以证明∠DAE=∠DEA=67.5°,推出DA=DE=2.)
故答案为2.
点评 本题考查正方形的性质、角平分线的性质定理、等腰三角形的判定等知识,解题的关键是灵活运用所学知识解决问题,利用计算角度的方法证明DA=DE比较简单,属于中考常考题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.下列运算中,正确的是( )
| A. | x3•x2•x=x5 | B. | x2+x2=2x4 | C. | (2x)2=2 x4 | D. | (x+m)(x-m)=x2-m2 |
16.科学家在实验中检测出某微生物约为0.0000025米,将0.0000025用科学记数法表示为( )
| A. | 2.5×10-6 | B. | 2.5×106 | C. | 2.5×10-5 | D. | 25×10-5 |
12.点A在数轴上到原点的距离为5,则A点表示的数为( )
| A. | 5 | B. | -5 | C. | 10 | D. | 5或-5 |