题目内容
1.方程组$\left\{\begin{array}{l}x+y=-6\\ xy=5\end{array}\right.$的解是$\left\{\begin{array}{l}{x=-5}\\{y=-1}\end{array}\right.$或$\left\{\begin{array}{l}{x=-1}\\{y=-5}\end{array}\right.$.分析 方程组利用加减消元法求出解即可.
解答 解:$\left\{\begin{array}{l}{x+y=-6①}\\{xy=5②}\end{array}\right.$,
由①得:y=-x-6③,
把③代入②得:x(-x-6)=5,
解得:x=-5或x=-1,
把x=-5代入③得:y=-1,把x=-1代入③得:y=-5,
则方程组的解为$\left\{\begin{array}{l}{x=-5}\\{y=-1}\end{array}\right.$或$\left\{\begin{array}{l}{x=-1}\\{y=-5}\end{array}\right.$,
故答案为:$\left\{\begin{array}{l}{x=-5}\\{y=-1}\end{array}\right.$或$\left\{\begin{array}{l}{x=-1}\\{y=-5}\end{array}\right.$
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
10.下列计算正确的是( )
| A. | (-3a2b)3=-3a5b3 | B. | $\frac{1}{2}$ab2•(-4a3b)=-2a4b3 | ||
| C. | 4m3n2÷m3n2=0 | D. | a5-a2=a3 |

 如图,点P是线段AB外一点,请用尺规求作点Q,使得四边形QPAB是平行四边形.(保留作图痕迹,不写作法).
如图,点P是线段AB外一点,请用尺规求作点Q,使得四边形QPAB是平行四边形.(保留作图痕迹,不写作法).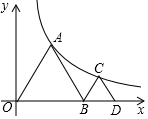 如图,△ADB、△BCD均为等边三角形,顶点A、C均在反比例函数y=$\frac{k}{x}$(x>0)图象上,若点A的坐标是(1,a),则点C的横坐标为1+$\sqrt{2}$.
如图,△ADB、△BCD均为等边三角形,顶点A、C均在反比例函数y=$\frac{k}{x}$(x>0)图象上,若点A的坐标是(1,a),则点C的横坐标为1+$\sqrt{2}$.