题目内容
9．
如图，在?ABCD中，AE=CG，求证：GF=HE．
分析 证明四边形AGCE是平行四边形，得出AG∥CE，证明四边形BEDG是平行四边形，得出BE∥DG，证出四边形EFGH是平行四边形，即可得出结论．
解答 证明：在?ABCD中，AD∥CB，AD=CB，
∵AE=CF，
∴四边形AGCE是平行四边形，
∴AG∥CE，
∴DE=DF，
∴四边形BEDG是平行四边形，
∴BE∥DG，
∴四边形EFGH是平行四边形，
∴GF=HE．
点评 此题主要考查了平行四边形的判定与性质，证明四边形是平行四边形是解决问题的关键．
练习册系列答案
相关题目
如图，AB是⊙O的直径，E为弦AC的延长线上一点，DE与⊙O相切于点D，且DE⊥AC，连结OD，若AB=10，AC=6，求DE的长．
17．
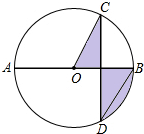如图，AB是⊙O的直径，弦CD⊥AB，∠CDB=30°，CD=2$\sqrt{3}$，则阴影部分图形的面积为（ ）
如图，AB是⊙O的直径，弦CD⊥AB，∠CDB=30°，CD=2$\sqrt{3}$，则阴影部分图形的面积为（ ）| A． | 4π | B． | 2π | C． | π | D． | $\frac{2π}{3}$ |
4．
已知函数y=ax2+bx+c（a≠0）的图象与函数y=x-$\frac{3}{2}$的图象如图所示，则下列结论：①ab＞0；②c＞-$\frac{3}{2}$；③a+b+c＜-$\frac{1}{2}$；④方程ax2+（b-1）x+c+$\frac{3}{2}$=0有两个不相等的实数根．其中正确的有（ ）
已知函数y=ax2+bx+c（a≠0）的图象与函数y=x-$\frac{3}{2}$的图象如图所示，则下列结论：①ab＞0；②c＞-$\frac{3}{2}$；③a+b+c＜-$\frac{1}{2}$；④方程ax2+（b-1）x+c+$\frac{3}{2}$=0有两个不相等的实数根．其中正确的有（ ）| A． | 4 个 | B． | 3 个 | C． | 2 个 | D． | 1 个 |
如图，AB是⊙O的直径，弦CD⊥AB于点E，AF是⊙O的切线，若AE=3，AF=CD，则FC是⊙O的切线．
12．
如图，?ABCD的对角线AC与BD相交于点O，AB⊥AC，若AB=4，∠ACB=30°，则BD的长是（ ）
如图，?ABCD的对角线AC与BD相交于点O，AB⊥AC，若AB=4，∠ACB=30°，则BD的长是（ ）| A． | 2$\sqrt{3}$ | B． | 2$\sqrt{7}$ | C． | 4$\sqrt{3}$ | D． | 4$\sqrt{7}$ |